题目内容
1.已知椭圆C1:y2a2y2a2+x2b2x2b2=1(a>b>0)的离心率e=√33√33,且经过点(1,√62√62),抛物线C2:x2=2py(p>0)的焦点F与椭圆C1的一个焦点重合.(Ⅰ)过F的直线与抛物线C2交于M,N两点,过M,N分别作抛物线C2的切线l1,l2,求直线l1,l2的交点Q的轨迹方程;
(Ⅱ)从圆O:x2+y2=5上任意一点P作椭圆C1的两条切线,切点为A,B,证明:∠APB为定值,并求出这个定值.
分析 (Ⅰ)设椭圆的半焦距为c,以及ca=√33ca=√33,设椭圆方程为y23c2+x22c2=1y23c2+x22c2=1,将点(1,√62)的坐标代入得c,然后求解椭圆方程,求出抛物线方程,设直线MN:y=kx+1,M(x1,y1),N(x2,y2),代入抛物线方程得x2-4kx-4=0,利用韦达定理结合函数的导数求解直线的斜率,直线方程,求出点Q的横坐标是12(x1+x2),点Q的纵坐标,然后求解点Q的轨迹方程.
(Ⅱ)①当两切线的之一的斜率不存在时,根据对称性,设点P在第一象限,求解∠APB的大小为定值.
②当两条切线的斜率都存在时,即x≠±√2时,设P(x0,y0),切线的斜率为k,则切线方程与椭圆方程联立,利用△=0,切线PA,PB的斜率k1,k2是上述方程的两个实根,通过k1k2=−y20−32−x20,求解∠APB的大小为定值π2.
解答 解:(Ⅰ)设椭圆的半焦距为c,则ca=√33,即a=√3c,则b=√2c,
椭圆方程为y23c2+x22c2=1,将点(1,√62)的坐标代入得c2=1,
故所求的椭圆方程为y23+x22=1焦点坐标为(0,±1),
故抛物线方程为x2=4y…(2分)
设直线MN:y=kx+1,M(x1,y1),N(x2,y2),代入抛物线方程得x2-4kx-4=0,
则x1+x2=4k,x1x2=-4,由于y=14x2,所以y′=12x,故直线l1的斜率为12x1,l1的方程为y−14x21=12x1(x−x1),即y=12x1x−14x21,
同理l2的方程为y=12x2x−14x22,
令12x1x−14x21=12x2x−14x22,即(x1−x2)x=12(x1−x2)(x1+x2),显然x1≠x2,
故x=12(x1+x2),即点Q的横坐标是12(x1+x2),
点Q的纵坐标是y=12x1x−14x21=14x1(x1+x2)−14x21=14x1x2=−1,即点Q(2k,-1),
故点Q的轨迹方程是y=-1…(4分)
(Ⅱ)证明:①当两切线的之一的斜率不存在时,根据对称性,设点P在第一象限,
则此时P点横坐标为√2,代入圆的方程得P点的纵坐标为√3,
此时两条切线方程分别为x=√2,y=√3,此时∠APB=π2,
若∠APB的大小为定值,则这个定值只能是π2…(5分)
②当两条切线的斜率都存在时,即x≠±√2时,设P(x0,y0),切线的斜率为k,
则切线方程为y-y0=k(x-x0),
与椭圆方程联立消元得(3+2k2)x2+4k(y0−kx0)x+2(kx0−y0)2−6=0…(6分)
由于直线y-y0=k(x-x0)是椭圆的切线,
故△=[4k(y0−kx0)]2−4(3+2k2)[2(kx0−y0)2−6]=0,
整理得(2−x20)k2+2x0y0k−(y20−3)=0…(8分)
切线PA,PB的斜率k1,k2是上述方程的两个实根,故k1k2=−y20−32−x20,…(10分)
点P在圆x2+y2=5上,故y20−3=2−x20,所以k1k2=-1,所以∠APB=π2.
综上可知:∠APB的大小为定值π2,得证…(12分)
点评 本题考查直线与椭圆的综合应用,椭圆以及抛物线的方程的求法,考查转化是以及计算能力.

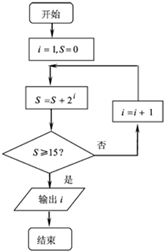
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | 非负数 | B. | 非正数 | C. | 正数 | D. | 不确定 |
