Question

18．求函数y=tanx+|tanx|的图象，并求出其定义域、单调区间及最小正周期．

Answer 1

分析 由条件化简函数的解析式，画出它的图象，数形结合可得结论．

解答 解：函数y=tanx+|tanx|=$\left\{\begin{array}{l}{0，x∈（kπ-\frac{π}{2}，kπ）}\\{2tanx，x∈[kπ，kπ+\frac{π}{2}）}\end{array}\right.$，它的图象如图所示：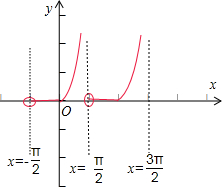

故函数y的定义域为{x|x≠kπ+$\frac{π}{2}$，k∈z}，单调增区间为[0，$\frac{π}{2}$），最小正周期为π．

点评 本题主要考查正切函数的图象特征，正切函数的定义域、单调性和周期性，属于基础题．