题目内容
9．化简cosα$\sqrt{\frac{1-sinα}{1+sina}}$+sinα$\sqrt{\frac{1-cosα}{1+cosα}}$（π＜α＜$\frac{3π}{2}$）得（ ）| A． | sinα+cosα-2 | B． | 2-sinα-cosα | C． | sinα-cosα | D． | cosα-sinα |
分析 利用同角三角函数基本关系式、三角函数值在各个象限的符号即可得出．
解答 解：∵π＜α＜$\frac{3π}{2}$，∴$\sqrt{\frac{1-sinα}{1+sinα}}$=$\sqrt{\frac{（1-sinα）^{2}}{1-si{n}^{2}α}}$=$\frac{1-sinα}{-cosα}$，
同理可得$\sqrt{\frac{1-cosα}{1+cosα}}$=$\frac{1-cosα}{-sinα}$，
∴原式=-（1-sinα）-（1-cosα）
=-2+cosα+sinα．
故选：A．
点评 本题考查了同角三角函数基本关系式、三角函数值在各个象限的符号，考查了计算能力，属于中档题．
练习册系列答案
相关题目
19．
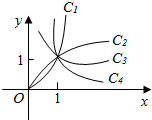已知幂函数y=xa在第一象限内的图象如图所示，a取±2，±$\frac{1}{2}$四个值，则相应的曲线C1，C2，C3，C4的a的值依次为（ ）
已知幂函数y=xa在第一象限内的图象如图所示，a取±2，±$\frac{1}{2}$四个值，则相应的曲线C1，C2，C3，C4的a的值依次为（ ）| A． | -2，-$\frac{1}{2}$，$\frac{1}{2}$，2 | B． | 2，$\frac{1}{2}$，-$\frac{1}{2}$，-2 | C． | -$\frac{1}{2}$，-2，2，$\frac{1}{2}$ | D． | 2，$\frac{1}{2}$，-2，-$\frac{1}{2}$ |
20．在△ABC中，角A，B，C的对边分别为a，b，c，m=（a2，b2），n=（tanA，tanB），且m∥n，那么△ABC一定是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | ||
| C． | 等腰三角形 | D． | 直角三角形或等腰三角形 |