题目内容
(本小题满分14分)
如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA⊥PD,E、F分别为PC、BD的中点。
(I)求证:直线EF//平面PAD;
(II)求证:直线EF⊥平面PDC。
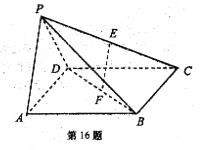
如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA⊥PD,E、F分别为PC、BD的中点。
(I)求证:直线EF//平面PAD;
(II)求证:直线EF⊥平面PDC。

略
证明:(I)连结AC,在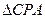 中,因为E,F分别为PC,AC的中点,
中,因为E,F分别为PC,AC的中点,
所 以EF//PA ………………3分
以EF//PA ………………3分
而PA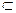 平面PAD,EF
平面PAD,EF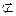 平面PAD,∴直
平面PAD,∴直 线EF//平面PAD ………………7分
线EF//平面PAD ………………7分
(II)因为面PAD⊥面ABCD,面PAD∩面ABCD=AD,
CD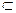 面ABCD,且CD⊥AD,所以CD⊥平面PAD,∴CD⊥PA …………10分
面ABCD,且CD⊥AD,所以CD⊥平面PAD,∴CD⊥PA …………10分
且CD、PD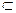 面PDC,所以PA⊥面PDC。 ………………12分
面PDC,所以PA⊥面PDC。 ………………12分
而EF//PA,所以直线EF⊥平面PDC ………………14分
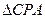 中,因为E,F分别为PC,AC的中点,
中,因为E,F分别为PC,AC的中点,所
 以EF//PA ………………3分
以EF//PA ………………3分而PA
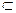 平面PAD,EF
平面PAD,EF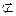 平面PAD,∴直
平面PAD,∴直 线EF//平面PAD ………………7分
线EF//平面PAD ………………7分(II)因为面PAD⊥面ABCD,面PAD∩面ABCD=AD,
CD
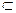 面ABCD,且CD⊥AD,所以CD⊥平面PAD,∴CD⊥PA …………10分
面ABCD,且CD⊥AD,所以CD⊥平面PAD,∴CD⊥PA …………10分且CD、PD
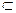 面PDC,所以PA⊥面PDC。 ………………12分
面PDC,所以PA⊥面PDC。 ………………12分而EF//PA,所以直线EF⊥平面PDC ………………14分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
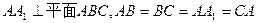 ,
,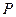 为
为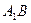 上的点.
上的点.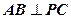 ;
;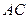 —
—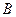 的大小为
的大小为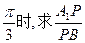 的值.
的值.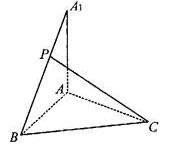
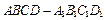 中,点
中,点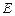 在棱
在棱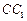 的延长线上,且
的延长线上,且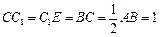 .
.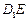 ∥平面
∥平面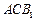 ;
;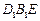
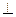 平面
平面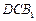 ;
; 的体积.
的体积.


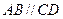 ,
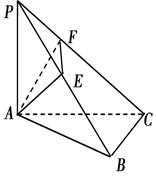
,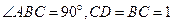 ,AB=2,E为AB的中点,将
,AB=2,E为AB的中点,将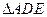 沿DE翻折至
沿DE翻折至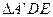 ,使二面角A
,使二面角A
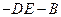 为直二面角。
为直二面角。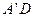 、
、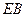 的中点,求证:
的中点,求证: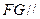 平面
平面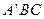 ;
;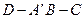 度数的余弦值
度数的余弦值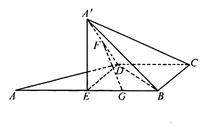
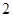 ,下底为
,下底为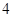 ,高为
,高为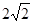 的等腰梯形,俯视图是两个半径分别为
的等腰梯形,俯视图是两个半径分别为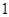 和
和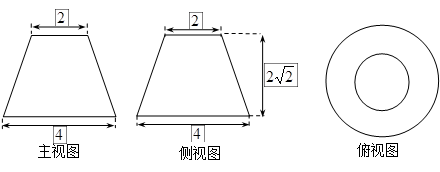
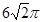
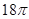
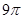
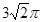
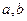 是两条不同的直线,
是两条不同的直线,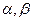 是两个不重合的平面,则下列命题中正确的是 ( )
是两个不重合的平面,则下列命题中正确的是 ( )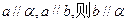
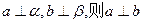
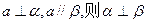
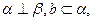 则
则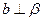
 D的棱长为1,棱AB//平面
D的棱长为1,棱AB//平面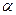 ,则正四面体上的所有点在平面
,则正四面体上的所有点在平面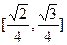
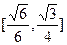
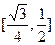
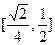
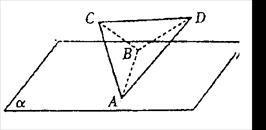
 、
、 ,两个不同的平面
,两个不同的平面 则下列命题中正确的是 ( )
则下列命题中正确的是 ( ) ,则
,则
 则
则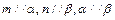 则
则
 则
则