题目内容
1.已知函数f(x)=lnx+$\frac{m}{x}$,m∈R.(1)若曲线y=f(x)在点(1,f(1))处的切线与y轴的交点的纵坐标为1,求m;
(2)讨论函数f(x)的单调区间;
(3)若对任意b>a>0,$\frac{f(b)-f(a)}{b-a}$<1恒成立,求m的取值范围.
分析 (1)求函数的导数,根据导数的几何意义即可求m;
(2)求函数的导数,利用导数即可研究f(x)的单调性;
(3)构造函数,求函数的导数,利用导数研究函数的最值即可
解答 解:(1)∵f′(x)=$\frac{1}{x}$-$\frac{m}{{x}^{2}}$,
∴f′(1)=1-m,又f(1)=m,
∴曲线y=f(x)在点(1,f(1)) 处的切线方程为:
y-m=(1-m)(x-1),
令x=0,得y=2m-1,
∴2m-1=1,解得m=1.
(2)易得函数 f(x)的定义域为(0,+∞)
由(1)知 f′(x)=$\frac{1}{x}$-$\frac{m}{{x}^{2}}$=$\frac{x-m}{{x}^{2}}$,
∴①当m≤0时,f′(x)>0恒成立,∴f(x)在(0,+∞) 单调递增;
②当m>0时,由f′(x)>0可得x>m,由f′(x)<0 可得0<x<m,
∴f(x)在(0,m)单调递减,在(m,+∞)单调递增.
综上所述,当m≤0时,f(x)在(0,+∞) 单调递增;
当m>0 时,f(x)在(0,m) 单 调递减,在 (m,+∞)单调递增.
(3)对任意b>a>0,$\frac{f(b)-f(a)}{b-a}$<1恒成立,
等价于f(b)-b<f(a)-a 恒成立.
设h(x)=f(x)-x=lnx+$\frac{m}{x}$-x(x>0),
则等价于h(x) 在(0,+∞) 上单调递减,
即h′(x)=$\frac{1}{x}$-$\frac{m}{{x}^{2}}$-1≤0 在(0,+∞) 恒成立,
∴m≥-x2+x(x>0)恒成立,
∵-x2+x=-(x-$\frac{1}{2}$)2+$\frac{1}{4}$,
∴(-x2+x)max=$\frac{1}{4}$,
∴m≥$\frac{1}{4}$(对m=$\frac{1}{4}$,h′(x)=0仅在x=$\frac{1}{4}$时成立),
则m的取值范围是[$\frac{1}{4}$,+∞).
点评 本题主要考查导数的几何意义以及函数最值的求解,利用导数的应用和分类讨论的思想方法是解决本题的关键.综合性较强,运算量较大,有一定的难度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (-2,-3) |
| A. | $f(2)<f(-\frac{3}{2})<f(-1)$ | B. | $f(-1)<f(-\frac{3}{2})<f(2)$ | C. | $f(2)<f(-1)<f(-\frac{3}{2})$ | D. | $f(-\frac{3}{2})<f(-1)<f(2)$ |
| A. | {x|x<-1或x>3} | B. | {x|-1<x<3} | C. | {x|x<-3或x>1} | D. | {x|-1<x<2或2<x<3} |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
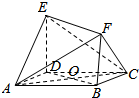 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,连结AC,AC∩BD=0,
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,连结AC,AC∩BD=0,