题目内容
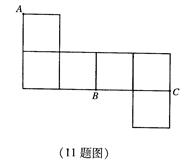
矩形ABCD(AB≤BC)中,AC=2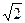 ,沿对角线AC把它折成直二面角B-AC-D后,BD=
,沿对角线AC把它折成直二面角B-AC-D后,BD=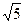 ,求AB、BC的长.
,求AB、BC的长.
翰林汇
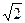 ,沿对角线AC把它折成直二面角B-AC-D后,BD=
,沿对角线AC把它折成直二面角B-AC-D后,BD=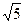 ,求AB、BC的长.
,求AB、BC的长. |
翰林汇
翰林汇AB=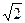 ,BC=
,BC=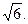
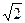 ,BC=
,BC=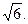
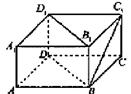
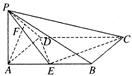
如图,
分别过B、D作BE⊥AC于E,DF⊥AC于F,
设∠BAC=θ,则AB=ACcosθ=2cosθ,
BE=DE=ABsinθ=sin2θ,
AE=ABcosθ=2cos2θ∴EF=AC-2AE
=2=-2cos2θ
折叠后,在平面ACD内过E作EG∥FD,且EG=FD,连接DG、BG、BD,则∠BEG为二面角B-AC-D的平面角,∴∠BEG=90°
于是BG=BE=sin2θ=2sin2θ
∴BG2+DG2=BD2,即:(2sin2θ)2+(-2cos2θ)2=5
∴4(cos2θ)2=1,∴cos2θ=±,
∵AB≤BC,∴cos2θ=-∴cosθ=,
故AB=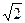 ,BC=
,BC=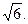
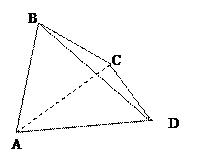 |
分别过B、D作BE⊥AC于E,DF⊥AC于F,
设∠BAC=θ,则AB=ACcosθ=2cosθ,
BE=DE=ABsinθ=sin2θ,
AE=ABcosθ=2cos2θ∴EF=AC-2AE
=2=-2cos2θ
折叠后,在平面ACD内过E作EG∥FD,且EG=FD,连接DG、BG、BD,则∠BEG为二面角B-AC-D的平面角,∴∠BEG=90°
于是BG=BE=sin2θ=2sin2θ
∴BG2+DG2=BD2,即:(2sin2θ)2+(-2cos2θ)2=5
∴4(cos2θ)2=1,∴cos2θ=±,
∵AB≤BC,∴cos2θ=-∴cosθ=,
故AB=
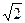 ,BC=
,BC=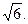

练习册系列答案
相关题目
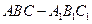 是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是
是正三棱柱(底面为正三角形,侧棱垂直于底面),它的底面边长和侧棱长都是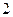 .
.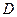 为侧棱
为侧棱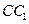 的中点,
的中点,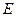 为底面一边
为底面一边 的中点.
的中点.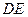 与
与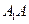 所成的角;
所成的角;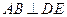 ;
;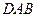 的距离.
的距离.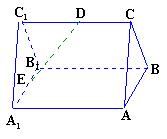
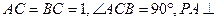 平面ABC,CE//PA,PA=2CE=2。
平面ABC,CE//PA,PA=2CE=2。 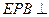 平面APB; (2)求二面角A—BE—P的正弦值。
平面APB; (2)求二面角A—BE—P的正弦值。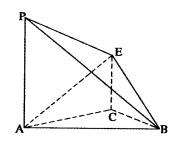
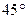 ,M为AB中点,N为SC中点.
,M为AB中点,N为SC中点.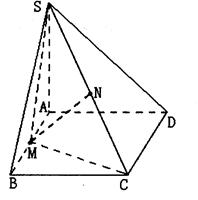
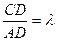 ,求实数
,求实数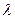 的值,使得直线SM与平面SCD所成角为
的值,使得直线SM与平面SCD所成角为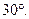
 为两条直线,
为两条直线, 为两个平面,下列四个命题中真命题是 ( )
为两个平面,下列四个命题中真命题是 ( ) 所成角相等,则
所成角相等,则



 平面
平面 =
= ,
, ,且
,且 ,二面角
,二面角 .
.  到平面
到平面 的大小为
的大小为 ,求
,求 的值.
的值.
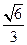
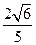
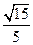
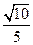
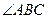 的度数为 .
的度数为 .