题目内容
(本小题满分12分)
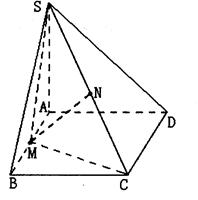
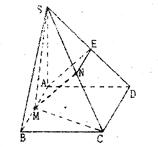
如图,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,二面角S—
CD—A的平面角为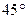 ,M为AB中点,N为SC中点.
,M为AB中点,N为SC中点.
(1)证明:MN//平面SAD;
(2)证明:平面SMC⊥平面SCD;
(3)若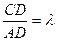 ,求实数
,求实数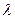 的值,使得直线SM与平面SCD所成角为
的值,使得直线SM与平面SCD所成角为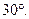
如图,在四棱锥S—ABCD中,底面ABCD为矩形,SA⊥平面ABCD,二面角S—
CD—A的平面角为
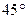 ,M为AB中点,N为SC中点.
,M为AB中点,N为SC中点.(1)证明:MN//平面SAD;
(2)证明:平面SMC⊥平面SCD;
|
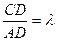 ,求实数
,求实数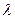 的值,使得直线SM与平面SCD所成角为
的值,使得直线SM与平面SCD所成角为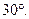
略
证明:取SD中点E,连接AE,NE,
则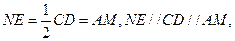
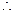 四边形AMNE为平行四边形,
四边形AMNE为平行四边形,
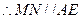 …………1分
…………1分
又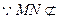 平面SAD …………3分
平面SAD …………3分
(2)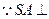 平面ABCD,
平面ABCD,
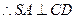 ,
,
 底面ABCD为矩形,
底面ABCD为矩形,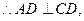
又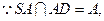
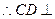 平面SAD,
平面SAD,
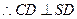
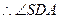 即为二面角S—CD—A的平面角,
即为二面角S—CD—A的平面角,
即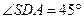 …………5分
…………5分
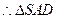 为等腰直角三角形,
为等腰直角三角形,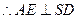
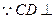 平面SAD,
平面SAD,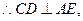
又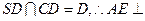 平面SCD
平面SCD
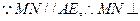 平面SCD,
平面SCD,
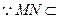 平面SMC,
平面SMC,
 平面SMC
平面SMC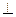 平面SCD …………8分
平面SCD …………8分
(3)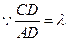 ,设AD=SA=a,则CD
,设AD=SA=a,则CD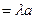
由(2)可得MN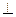 平面SCD,
平面SCD,
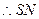 即为SM在平面SCD内的射影
即为SM在平面SCD内的射影
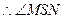 即为直线SM与平面SCD所成角,
即为直线SM与平面SCD所成角,
即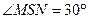 …………9分
…………9分
而MN=AE=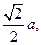
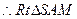 中,
中,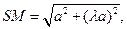 而
而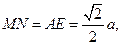
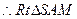 中,由
中,由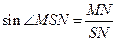 得
得
 解得
解得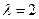
当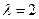 时,直线SM与平面SCD所成角为
时,直线SM与平面SCD所成角为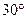 …………12分
…………12分
|
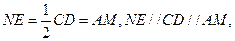
 四边形AMNE为平行四边形,
四边形AMNE为平行四边形,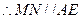 …………1分
…………1分又
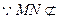 平面SAD …………3分
平面SAD …………3分(2)
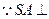 平面ABCD,
平面ABCD,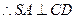 ,
,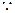 底面ABCD为矩形,
底面ABCD为矩形,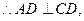
又
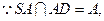
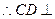 平面SAD,
平面SAD,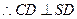
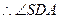 即为二面角S—CD—A的平面角,
即为二面角S—CD—A的平面角,即
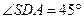 …………5分
…………5分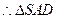 为等腰直角三角形,
为等腰直角三角形,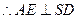
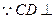 平面SAD,
平面SAD,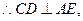
又
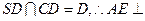 平面SCD
平面SCD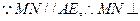 平面SCD,
平面SCD,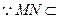 平面SMC,
平面SMC,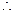 平面SMC
平面SMC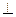 平面SCD …………8分
平面SCD …………8分(3)
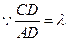 ,设AD=SA=a,则CD
,设AD=SA=a,则CD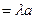
由(2)可得MN
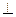 平面SCD,
平面SCD,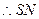 即为SM在平面SCD内的射影
即为SM在平面SCD内的射影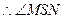 即为直线SM与平面SCD所成角,
即为直线SM与平面SCD所成角,即
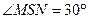 …………9分
…………9分而MN=AE=
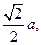
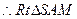 中,
中,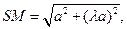 而
而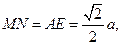
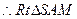 中,由
中,由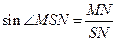 得
得 解得
解得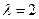
当
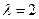 时,直线SM与平面SCD所成角为
时,直线SM与平面SCD所成角为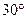 …………12分
…………12分
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
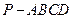 的底面
的底面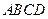 是边长为1的菱形,
是边长为1的菱形,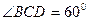 ,
,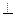 底面ABCD,
底面ABCD,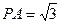 。
。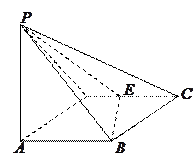
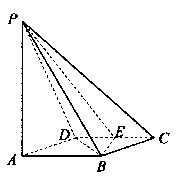
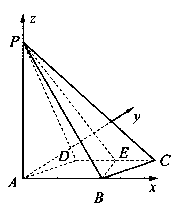
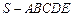 中,
中,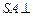 底面
底面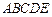 ,
,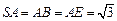 ,
,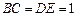 ,
,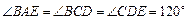 。
。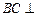 平面
平面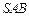 ;
;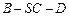 的余弦值。
的余弦值。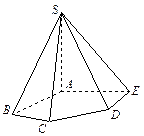

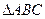
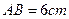
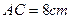
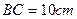
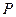
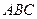
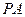 与平面
与平面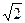 ,沿对角线AC把它折成直二面角B-AC-D后,BD=
,沿对角线AC把它折成直二面角B-AC-D后,BD=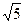 ,求AB、BC的长.
,求AB、BC的长.
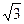 的菱形,∠BAD=60°,侧面VAD⊥底面ABCD,VA=VD,E为AD的中点.
的菱形,∠BAD=60°,侧面VAD⊥底面ABCD,VA=VD,E为AD的中点.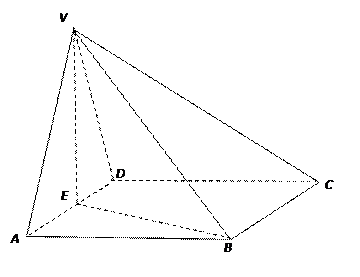
 系是( )
系是( ) ABCD
ABCD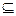 平面ABCD
平面ABCD ,有下面四个命题:
,有下面四个命题: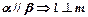 ; (2)
; (2)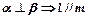 ;
; 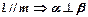 ; (4)
; (4)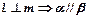 .
.