题目内容
如图所示,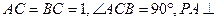 平面ABC,CE//PA,PA=2CE=2。
平面ABC,CE//PA,PA=2CE=2。
(1)求证:平面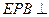 平面APB; (2)求二面角A—BE—P的正弦值。
平面APB; (2)求二面角A—BE—P的正弦值。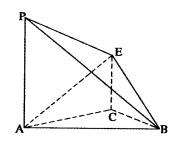
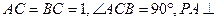 平面ABC,CE//PA,PA=2CE=2。
平面ABC,CE//PA,PA=2CE=2。 (1)求证:平面
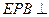 平面APB; (2)求二面角A—BE—P的正弦值。
平面APB; (2)求二面角A—BE—P的正弦值。
(Ⅰ) 见解析 (Ⅱ)
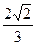
(1)取AB,PB的中点G,F连接CG,GF,FE,
则GF//PA,且
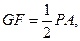 又CE//PA,
又CE//PA,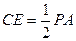 ,
,所以CE//GF,且CE=GF,所以四边形GFEC是平行四边形,
所以EF//CG。,又AC=BC,AG=GB,
所以
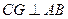 ,又PA
,又PA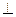 面ABC,得CG
面ABC,得CG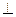 PA,
PA,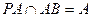 ,
,所以,CG
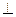 面PAB,因此,EF
面PAB,因此,EF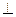 面PAB,又
面PAB,又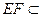 面EPB,
面EPB,所以平面EPB
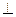 平面APB。
平面APB。 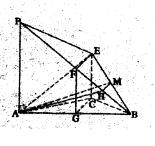 (2)在平面PAB内过点A作AB
(2)在平面PAB内过点A作AB PB于点H,
PB于点H,因为平面EPB
 平面APB,
平面APB,又平面EPB
 平面APB=PB,
平面APB=PB,所以AH
 平面EPB,取EB的中点M,
平面EPB,取EB的中点M,连接AM,
 MH, 因
MH, 因 为AB=AE=
为AB=AE=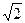 , 所以AM
, 所以AM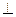 EB,
EB,故由三垂线定理的逆定理可知,HM
 EB,
EB,因此
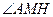 为二面角A—BE—P的平面角。
为二面角A—BE—P的平面角。 在
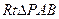 ,PA=2,
,PA=2,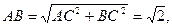
所以
 在
在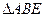 中,AB=BE=EA=
中,AB=BE=EA=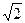 ,
,所以
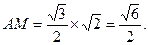
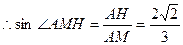
因此,二面角A—BE—P的正弦值为
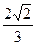

练习册系列答案
相关题目
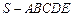 中,
中,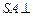 底面
底面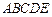 ,
,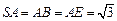 ,
,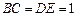 ,
,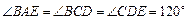 。
。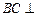 平面
平面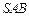 ;
;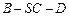 的余弦值。
的余弦值。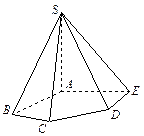
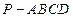 中,面
中,面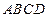 为矩形,
为矩形,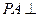 面
面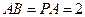
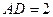 时,平面PBD⊥平面PAC;
时,平面PBD⊥平面PAC;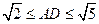 时,求二面角
时,求二面角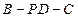 的取值范围。
的取值范围。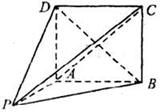
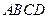 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于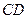 ,线段
,线段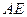 垂直于圆
垂直于圆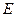 是圆
是圆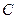 、
、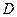 的点,
的点,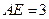 ,圆
,圆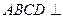 平面
平面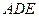 ;
;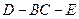 的平面角的正切值.
的平面角的正切值.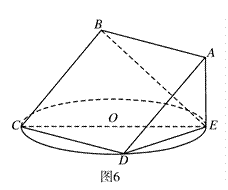
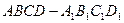 中,点
中,点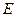 在棱
在棱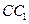 的延长线上,
的延长线上,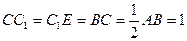 .
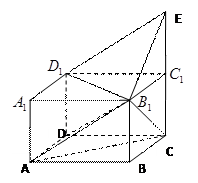
.
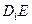 //平面
//平面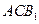 ;
; (Ⅱ) 求证:平面
(Ⅱ) 求证:平面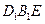
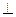 平面
平面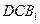 ;
;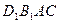 的体积.
的体积. 中,
中, 是
是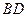 的中点,
的中点,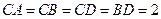 ,
,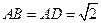 .(Ⅰ)求证:
.(Ⅰ)求证: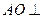 平面
平面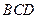 ;(Ⅱ)求异面直线
;(Ⅱ)求异面直线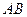 与
与 所成角的大小;
所成角的大小;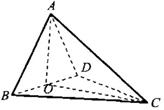
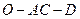 的大小.
的大小.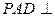 平面ABCD,ABCD为正方形,
平面ABCD,ABCD为正方形,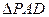 是直角三角形,且
是直角三角形,且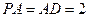 ,E、F、G分别是线段PA,PD,CD的中点.
,E、F、G分别是线段PA,PD,CD的中点.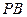 ∥面EFC;
∥面EFC;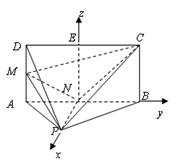
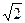 ,沿对角线AC把它折成直二面角B-AC-D后,BD=
,沿对角线AC把它折成直二面角B-AC-D后,BD=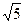 ,求AB、BC的长.
,求AB、BC的长.
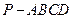 中,
中,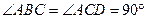 ,
,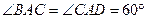 ,
,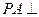 底面
底面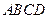 ,
,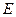 为
为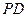 的中点,
的中点,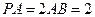 .
.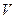 ;
;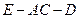 的大小.
的大小.