题目内容
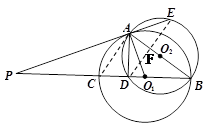
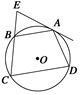
如图,圆O1与圆O2相交于A、B两点,AB是圆O2的直径,过A点作圆O1的切线交圆O2于点E,并与BO1的延长线交于点P,PB分别与圆O1、圆O2交于C,D两点。
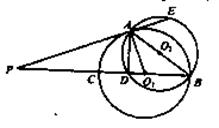
求证:(Ⅰ)PA·PD=PE·PC;
(Ⅱ)AD=AE。

求证:(Ⅰ)PA·PD=PE·PC;
(Ⅱ)AD=AE。
(Ⅰ)见解析 (Ⅱ)见解析
本试题主要考查了平面中圆与直线的位置关系 综合而运用,以及三三角形相似的运用。
(1)利用圆内的切割线定理得到结论即可
(2)利用垂直关系,和同弧所对的圆周角相等的性质得到结论
(Ⅰ)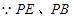 分别是⊙
分别是⊙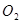 的割线∴
的割线∴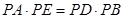 ① (2分)
① (2分)
又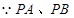 分别是⊙
分别是⊙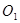 的切线和割线∴
的切线和割线∴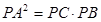 ② (4分)
② (4分)
由①,②得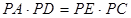 (5分)
(5分)
(Ⅱ)连结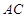 、
、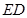 设
设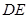 与
与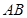 相交于点
相交于点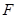 ∵
∵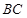 是⊙
是⊙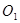 的直径∴
的直径∴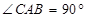
∴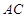 是⊙
是⊙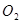 的切线. (6分)
的切线. (6分)
由(Ⅰ)知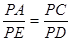 ,∴
,∴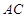 ∥
∥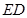 ∴
∴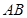 ⊥
⊥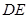 ,
, 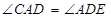 (8分)
(8分)
又∵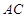 是⊙
是⊙ 的切线,∴
的切线,∴ 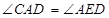 又
又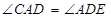 ,∴
,∴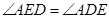 ∴
∴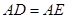
(1)利用圆内的切割线定理得到结论即可
(2)利用垂直关系,和同弧所对的圆周角相等的性质得到结论
(Ⅰ)
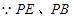 分别是⊙
分别是⊙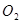 的割线∴
的割线∴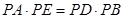 ① (2分)
① (2分)又
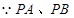 分别是⊙
分别是⊙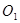 的切线和割线∴
的切线和割线∴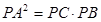 ② (4分)
② (4分)由①,②得
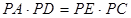 (5分)
(5分)
(Ⅱ)连结
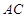 、
、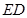 设
设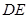 与
与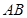 相交于点
相交于点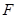 ∵
∵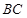 是⊙
是⊙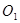 的直径∴
的直径∴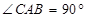
∴
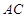 是⊙
是⊙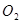 的切线. (6分)
的切线. (6分)由(Ⅰ)知
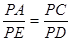 ,∴
,∴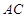 ∥
∥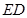 ∴
∴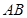 ⊥
⊥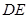 ,
, 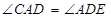 (8分)
(8分)又∵
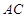 是⊙
是⊙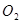 的切线,∴
的切线,∴ 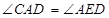 又
又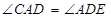 ,∴
,∴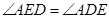 ∴
∴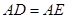

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 内切于点T,P是外圆
内切于点T,P是外圆 上任意一点,连PT交
上任意一点,连PT交 于点M,PN与内圆
于点M,PN与内圆
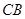 是⊙
是⊙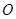 的直径,
的直径,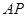 是⊙
是⊙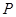 ,
,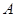 为切点.若
为切点.若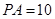 ,
,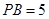 ,
,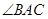 的平分线
的平分线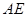 与
与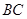 和⊙
和⊙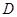 、
、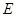 ,则
,则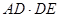 的值为( )
的值为( )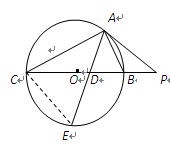
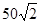
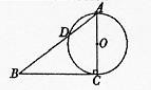
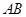 是⊙
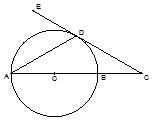
是⊙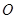 的直径,直线
的直径,直线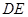 切⊙
切⊙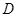 ,且与
,且与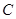 ,若
,若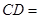
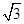 ,
,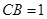 ,则
,则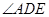 = .
= .
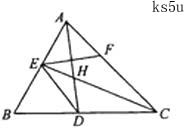
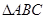 中的两条角平分线
中的两条角平分线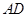 和
和 相交于
相交于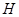 ,
,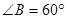 ,
,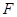 在
在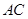 上,且
上,且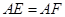 。
。 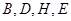 四点共圆;
四点共圆;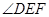 。
。
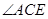 =
=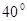 ,
,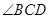 = .
= . 