题目内容
选修4-1:几何证明选讲(本小题满分10分)
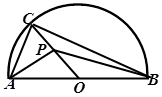
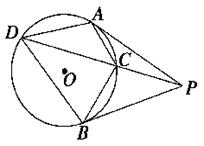
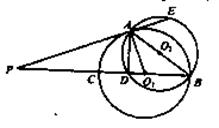
如图, 半径分别为R,r(R>r>0)的两圆 内切于点T,P是外圆
内切于点T,P是外圆 上任意一点,连PT交
上任意一点,连PT交 于点M,PN与内圆
于点M,PN与内圆 相切,切点为N。求证:PN:PM为定值。
相切,切点为N。求证:PN:PM为定值。
如图, 半径分别为R,r(R>r>0)的两圆
 内切于点T,P是外圆
内切于点T,P是外圆 上任意一点,连PT交
上任意一点,连PT交 于点M,PN与内圆
于点M,PN与内圆 相切,切点为N。求证:PN:PM为定值。
相切,切点为N。求证:PN:PM为定值。
见解析。
本试题主要是考查了平面几何性质的运用。三角形的相似,以及圆的公切线概念和性质运用,首先根据作两圆的公切线TQ,连接OP,O1M,D得到线段比例关系,然后由由弦切角定理得到角想的呢过,并利用平行关系,故可证明。
作两圆的公切线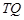 ,连结
,连结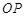 ,
,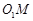 ,
,
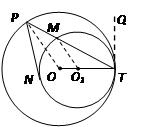
则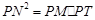 ,所以
,所以 .………3分
.………3分
由弦切角定理知,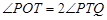 ,
,
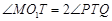 ,于是
,于是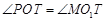 ,
,
所以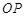 ∥
∥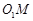 ,………………6分
,………………6分
所以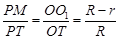 ,所以
,所以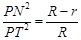 , ……………………………………8分
, ……………………………………8分
所以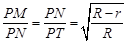 为定值. ………………………………………………10分
为定值. ………………………………………………10分
作两圆的公切线
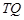 ,连结
,连结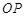 ,
,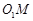 ,
,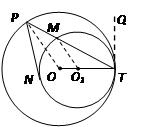
则
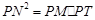 ,所以
,所以 .………3分
.………3分由弦切角定理知,
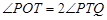 ,
,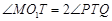 ,于是
,于是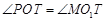 ,
,所以
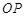 ∥
∥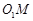 ,………………6分
,………………6分所以
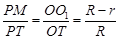 ,所以
,所以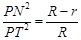 , ……………………………………8分
, ……………………………………8分所以
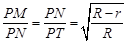 为定值. ………………………………………………10分
为定值. ………………………………………………10分
练习册系列答案
相关题目
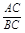 =
=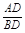 .
.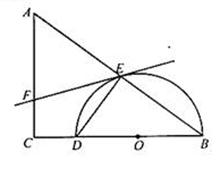
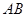 为⊙
为⊙ 的直径,
的直径,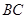 切⊙
切⊙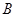 ,
,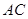 交⊙
交⊙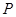 ,
,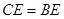 ,点
,点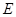 在
在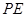 是⊙
是⊙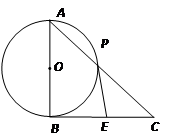

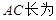 ( )
( )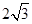
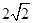

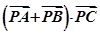 的最小值为 .
的最小值为 .