Question

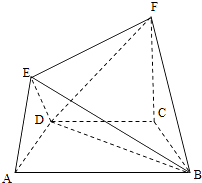
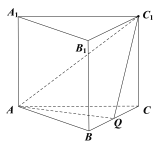
【题目】如图，在正三棱柱（底面为正三角形的直棱柱）ABC-A1B1C1中，已知AB=AA1=2，点Q为BC的中点．

（Ⅰ）求证：平面平面；

（Ⅱ）求点到平面AQC1的距离．

Answer 1

【答案】（Ⅰ ）见解析（Ⅱ）

【解析】分析：（Ⅰ）由等腰三角形的性质可得，由线面垂直的性质可得，从而可得平面，由面面垂直的判定定理可得结果；（Ⅱ）设点到平面AQC1的距离为，由（I）知，平面，则,，，利用可得结果.

详解：（I）由题意知：，为的中点，∴.

由平面得：

∵平面，且

∴平面，又∵平面，∴平面平面

（II）设点到平面AQC1的距离为，

在正三棱柱ABC-A1B1C1中，平面，故为三棱锥 C1-ABQ的高。

由（I）知，平面，则,易求得

故，

因为，所以，

即，则