题目内容
【题目】如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时, ![]() 的坐标为 .
的坐标为 . 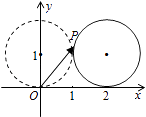
【答案】(2﹣sin2,1﹣cos2)
【解析】解:设滚动后的圆的圆心为O',切点为A(2,0),连接O'P,
过O'作与x轴正方向平行的射线,交圆O'于B(3,1),设∠BO'P=θ
∵⊙O'的方程为(x﹣2)2+(y﹣1)2=1,
∴根据圆的参数方程,得P的坐标为(2+cosθ,1+sinθ),
∵单位圆的圆心的初始位置在(0,1),圆滚动到圆心位于(2,1)
∴∠AO'P=2,可得θ= ![]() ﹣2
﹣2
可得cosθ=cos( ![]() ﹣2)=﹣sin2,sinθ=sin(
﹣2)=﹣sin2,sinθ=sin( ![]() ﹣2)=﹣cos2,
﹣2)=﹣cos2,
代入上面所得的式子,得到P的坐标为(2﹣sin2,1﹣cos2)
∴ ![]() 的坐标为(2﹣sin2,1﹣cos2).
的坐标为(2﹣sin2,1﹣cos2).
所以答案是:(2﹣sin2,1﹣cos2)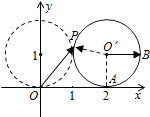
【考点精析】利用圆的参数方程对题目进行判断即可得到答案,需要熟知圆![]() 的参数方程可表示为
的参数方程可表示为![]() .
.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案【题目】某校为了解高二学生![]() 、
、![]() 两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试![]() 、
、![]() 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2![]() 2列联表:
2列联表:
|
| 合计 | |
| 40 | 20 | 60 |
| 20 | 30 | 50 |
合计 | 60 | 50 | 110 |
(1)据此表格资料,能否在犯错的概率不超过0.01的前提下认为“![]() 学科合格”与“
学科合格”与“![]() 学科合格”有关;
学科合格”有关;
(2)从“![]() 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“![]() 学科合格”的人数为
学科合格”的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附公式与表:![]()
【题目】某地铁换乘站设有编号为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
安全出口编号 |
|
|
|
|
|
疏散乘客时间( | 186 | 125 | 160 | 175 | 145 |
则疏散乘客最快的一个安全出口的编号是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()