题目内容
【题目】如图,动点M到两定点A(﹣1,0)、B(2,0)构成△MAB,且∠MBA=2∠MAB,设动点M的轨迹为C. 
(1)求轨迹C的方程;
(2)设直线y=﹣2x+m与y轴交于点P,与轨迹C相交于点Q、R,且|PQ|<|PR|,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:设M的坐标为(x,y),显然有x>0,且y≠0
当∠MBA=90°时,点M的坐标为(2,±3)
当∠MBA≠90°时,x≠2,由∠MBA=2∠MAB有tan∠MBA= ![]() ,
,
化简可得3x2﹣y2﹣3=0
而点(2,±3)在曲线3x2﹣y2﹣3=0上
综上可知,轨迹C的方程为3x2﹣y2﹣3=0(x>1);
(2)解:直线y=﹣2x+m与3x2﹣y2﹣3=0(x>1)联立,消元可得x2﹣4mx+m2+3=0①
∴①有两根且均在(1,+∞)内
设f(x)=x2﹣4mx+m2+3,∴ 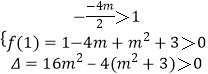 ,∴m>1,m≠2
,∴m>1,m≠2
设Q,R的坐标分别为(xQ,yQ),(xR,yR),
∵|PQ|<|PR|,∴xR=2m+ ![]() ,xQ=2m﹣
,xQ=2m﹣ ![]() ,
,
∴ ![]() =
= ![]() =
= ![]()
∵m>1,且m≠2
∴ ![]() ,且
,且 ![]()
∴ ![]() ,且
,且 ![]()
∴ ![]() 的取值范围是(1,7)∪(7,7+4
的取值范围是(1,7)∪(7,7+4 ![]() )
)
【解析】(1)设出点M(x,y),分类讨论,根据∠MBA=2∠MAB,利用正切函数公式,建立方程化简即可得到点M的轨迹方程;(2)直线y=﹣2x+m与3x2﹣y2﹣3=0(x>1)联立,消元可得x2﹣4mx+m2+3=0①,利用①有两根且均在(1,+∞)内可知,m>1,m≠2设Q,R的坐标,求出xR , xQ , 利用 ![]() ,即可确定
,即可确定 ![]() 的取值范围.
的取值范围.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目