题目内容
【题目】如图 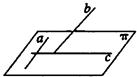
(1)证明命题“a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥b,则a⊥c”为真.
(2)写出上述命题的逆命题,并判断其真假(不需要证明)
【答案】
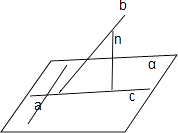
(1)证明:证法一:如图,过直线b上任一点作平面α的垂线n,设直线a,b,c,n对应的方向向量分别是 ![]() ,则
,则 ![]() 共面,
共面,
根据平面向量基本定理,存在实数λ,μ使得 ![]() ,
,
则 ![]() =
= ![]()
因为a⊥b,所以 ![]() ,
,
又因为aα,n⊥α,
所以 ![]() ,
,
故 ![]() ,从而a⊥c
,从而a⊥c
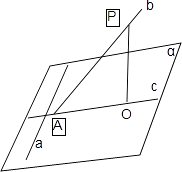
证法二
如图,记c∩b=A,P为直线b上异于点A的任意一点,过P做PO⊥π,垂足为O,则O∈c,
∵PO⊥π,aπ,
∴直线PO⊥a,
又a⊥b,b平面PAO,PO∩b=P,
∴a⊥平面PAO,
又c平面PAO,
∴a⊥c
(2)证明:逆命题为:a是平面π内的一条直线,b是π外的一条直线(b不垂直于π),c是直线b在π上的投影,若a⊥c,则a⊥b,
逆命题为真命题
【解析】(1)证法一:做出辅助线,在直线上构造对应的方向向量,要证两条直线垂直,只要证明两条直线对应的向量的数量积等于0,根据向量的运算法则得到结果.
证法二:做出辅助线,根据线面垂直的性质,得到线线垂直,根据线面垂直的判定定理,得到线面垂直,再根据性质得到结论.(2)把所给的命题的题设和结论交换位置,得到原命题的逆命题,判断出你命题的正确性.
【考点精析】通过灵活运用四种命题和向量语言表述线线的垂直、平行关系,掌握原命题:若P则q; 逆命题:若q则p;否命题:若┑P则┑q;逆否命题:若┑q则┑p;设直线![]() 的方向向量分别是
的方向向量分别是![]() ,则要证明
,则要证明![]() ∥
∥![]() ,只需证明
,只需证明![]() ∥
∥![]() ,即
,即![]() ;则要证明
;则要证明![]() ,只需证明
,只需证明![]() ,即
,即![]() 即可以解答此题.
即可以解答此题.

【题目】某校为了解高二学生![]() 、
、![]() 两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试
两个学科学习成绩的合格情况是否有关,随机抽取了该年级一次期末考试![]() 、
、![]() 两个学科的合格人数与不合格人数,得到以下2
两个学科的合格人数与不合格人数,得到以下2![]() 2列联表:
2列联表:
|
| 合计 | |
| 40 | 20 | 60 |
| 20 | 30 | 50 |
合计 | 60 | 50 | 110 |
(1)据此表格资料,能否在犯错的概率不超过0.01的前提下认为“![]() 学科合格”与“
学科合格”与“![]() 学科合格”有关;
学科合格”有关;
(2)从“![]() 学科合格”的学生中任意抽取2人,记被抽取的2名学生中“
学科合格”的学生中任意抽取2人,记被抽取的2名学生中“![]() 学科合格”的人数为
学科合格”的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附公式与表:![]()