题目内容
【题目】已知中心在原点的双曲线C的渐近线方程为y=±2x,且该双曲线过点(2,2).
(1)求双曲线C的标准方程;
(2)点A为双曲线C上任一点,F1F2分别为双曲线的左右焦点,过其中的一个焦点作∠F1AF2的角平分线的垂线,垂足为点P,求点P的轨迹方程.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)根据渐近线方程,设出双曲线方程,根据点在双曲线上,求出参数值,即可得到结果;
(2)根据题意,由三角形全等,结合双曲线的定义,推出点![]() 满足的条件,根据圆的定义,即可写出其轨迹方程.
满足的条件,根据圆的定义,即可写出其轨迹方程.
(1)根据题意,双曲线的渐近线方程是y=±2x,
则设双曲线方程为:4x2﹣y2=λ,(λ≠0),
点(2,2)代入得:λ=12,
则双曲线方程为:4x2﹣y2=12,
即![]() 1.
1.
(2)∵F1,F2是双曲线![]() 1的左右焦点,
1的左右焦点,
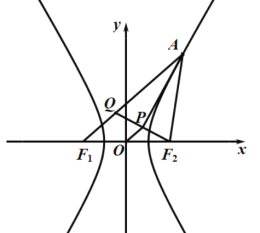
过F2作角的平分线AB的垂线,垂足为P,
并且交AF1于Q,连接OP,
如下图所示:
则![]() //
//![]() ,
,
显然![]()
故|AQ|=|AF2|,
∴|F1Q|=|AF1|﹣|AQ|=|AF1|﹣|AF2|=2a,
∴|OP|=a![]() ,
,
由圆的定义可知,点P的轨迹是以点O为圆心,![]() 为半径的圆,
为半径的圆,
所以P的轨迹方程为:x2+y2=3.

练习册系列答案
相关题目




