��Ŀ����
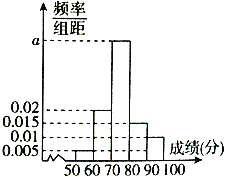
����Ŀ��Ϊ���˽�ijѧУ�߶��꼶ѧ���������ɼ������г�ȡn��ѧ���������ɼ����ٷ��ƣ���Ϊ���������ɼ��ֳ� 5�飺[50��60����[60��70����[70��80����[80��90����[90��100]��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ���ɼ�����[70��80���е�����Ϊ20��
���� | Ů�� | �ϼ� | |
���� | |||
������ | |||
�ϼ� |
������a��n��ֵ��
�������������������˼�룬���Ƹ�У�߶�ѧ�������ɼ���ƽ����![]() ����λ��m��
�����m��
���ɼ���80�����ϣ���80�֣�Ϊ���㣬�����гɼ�����[50��80���е��С�Ů��������Ϊ1��2���ɼ�����[80��100]�е��С�Ů��������Ϊ3��2�����2��2�����������ж��Ƿ���95%�İ�����Ϊ�����ɼ��������Ա��йأ�
�ο���ʽ�����ݣ�K2=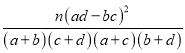 ��
��
P��K2��k�� | 0.50 | 0.05 | 0.025 | 0.005 |
k | 0.455 | 3.841 | 5.024 | 7.879 |
���𰸡���1��a=0.05,n=40��2��m=75��3��û��95%�İ�����Ϊ�����ɼ��������Ա��й�
�������������������1������С�����ε������Ϊ1���![]() ��Ȼ�����
��Ȼ�����![]() ��n����2�����ø�����м�ֵ��Ƶ�ʵij˻�����ƽ������������λ����Ƶ�ʷֲ�ֱ��ͼ��Ϊ�����ȵ�����������λ������3����������д�����������ݹ�ʽ���K2,���òο����ݽ����жϡ�
��n����2�����ø�����м�ֵ��Ƶ�ʵij˻�����ƽ������������λ����Ƶ�ʷֲ�ֱ��ͼ��Ϊ�����ȵ�����������λ������3����������д�����������ݹ�ʽ���K2,���òο����ݽ����жϡ�
���������
����������ɵ�
10a=1����0.005+0.01+0.015+0.02����10��
��a=0.05��
�� n=![]() =40
=40
���������⣬�����Ƶ�ʷֱ�Ϊ0.05��0.2��0.5��0.15��0.1��
��![]() =55��0.05+65��0.2+75��0.5+85��0.15+95��0.1=75.5��
=55��0.05+65��0.2+75��0.5+85��0.15+95��0.1=75.5��
����λ��Ϊm��
��m��70����0.05=0.5����0.05+0.2����
��m=75��
���������⣬���������Ϊ6�ˣ�Ů��Ϊ4�ˣ������������Ϊ10�ˣ�Ů��Ϊ20�ˣ�
2��2������
���� | Ů�� | �ϼ� | |
���� | 6 | 4 | 10 |
������ | 10 | 20 | 30 |
�ϼ� | 16 | 24 | 40 |
�ɱ��ɵ�
K2=![]() ��2.222��3.841��
��2.222��3.841��
��û��95%�İ�����Ϊ�����ɼ��������Ա��йأ�

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�