题目内容
【题目】在四棱锥P﹣ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分别为PB,PC中点.
(Ⅰ)求证:MN∥平面PAD;
(Ⅱ)求二面角B﹣AM﹣C的大小;
(Ⅲ)在BC上是否存在点E,使得EN⊥平面AMN?若存在,求 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】证明:(Ⅰ)∵M,N分别是PB,PC中点 ∴MN是△ABC的中位线
∴MN∥BC∥AD
又∵AD平面PAD,MN平面PAD
所以MN∥平面PAD.
解:(Ⅱ)过点P作PO垂直于AB,交AB于点O,
因为平面PAB⊥平面ABCD,所以PO⊥平面ABCD,
如图建立空间直角坐标系,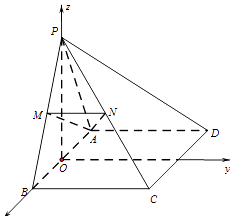
设AB=2,则A(﹣1,0,0),C(1,1,0),
M( ![]() ,0,
,0, ![]() ),
),
B(1,0,0),N( ![]() ,
, ![]() ,
, ![]() ),
),
则 ![]() ,
, 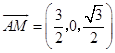
设平面CAM法向量为 ![]() ,
,
由 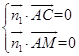 ,得
,得 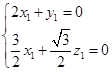 ,
,
令x1=1,则 ![]() ,即
,即 ![]()
平面ABM法向量 ![]()
所以,二面角B﹣AM﹣C的余弦值 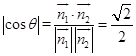
因为二面角B﹣AM﹣C是锐二面角,
所以二面角B﹣AM﹣C等于45°
(Ⅲ)存在点E,使得EN⊥平面AMN
设E(1,λ,0),则  ,
,
由 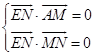 可得
可得 ![]() ,
,
所以在BC存在点E,使得EN⊥平面AMN,
此时 ![]() .
.
【解析】(本小题满分14分)
【考点精析】本题主要考查了直线与平面平行的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能正确解答此题.

【题目】某校举行环保知识竞赛,为了了解本次竞赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为正数,满分100分),进行统计,请根据频率分布表中所提供的数据,解答下列问题:
(Ⅰ)求a、b的值;
(Ⅱ)若从成绩较好的第3、4、5组中,按分层抽样的方法抽取6人参加社区志愿者活动,并从中选出2人做负责人,求2人中至少有1人是第四组的概率.
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60] | 5 | 0.05 |
第2组 | [60,70] | a | 0.35 |
第3组 | [70,80] | 30 | b |
第4组 | [80,90] | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 | |
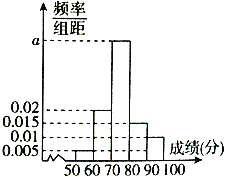
【题目】为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示.成绩落在[70,80)中的人数为20.
男生 | 女生 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(Ⅰ)求a和n的值;
(Ⅱ)根据样本估计总体的思想,估计该校高二学生物理成绩的平均数![]() 和中位数m;
和中位数m;
(Ⅲ)成绩在80分以上(含80分)为优秀,样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,完成2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=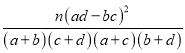 .
.
P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
k | 0.455 | 3.841 | 5.024 | 7.879 |