题目内容
【题目】如图,边长为3的正方形![]() 所在平面与等腰直角三角形
所在平面与等腰直角三角形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,且
,且![]() ,
, ![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.

【答案】(Ⅰ)证明见解析 (Ⅱ)所求二面角的余弦值为![]()
【解析】试题分析:(Ⅰ)考查的是直线与平面平行的判定定理.添加辅助线证明过程中可知![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以只需重点是证明
,所以只需重点是证明![]() (Ⅱ)考查的是利用平面法向量求二面角的方法.观察图象结合已知可知
(Ⅱ)考查的是利用平面法向量求二面角的方法.观察图象结合已知可知![]() 刚好可建立一个坐标系,从而可得
刚好可建立一个坐标系,从而可得 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,进而可得
,进而可得![]() 的法向量
的法向量![]() 和
和![]() 的法向量
的法向量![]() ,最后利用公式
,最后利用公式![]() 求出二面角的余弦值.
求出二面角的余弦值.
试题解析:
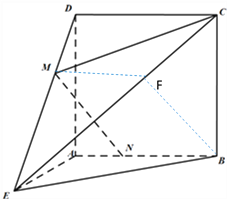
(Ⅰ)过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() 因为
因为![]() ,
, ![]() ,所以
,所以![]() 又
又![]() ,所以
,所以![]() 故
故![]() ,
,
所以四边形![]() 为平行四边形,故
为平行四边形,故![]() ,
,
而![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
(Ⅱ)以![]() 为坐标原点,
为坐标原点, ![]() 所在方向为
所在方向为![]() 轴正方向,建立平面直角坐标系,
轴正方向,建立平面直角坐标系,
则![]() ,
, ![]() ,
, ![]() ,
, ![]()
平面![]() 的法向量为
的法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则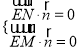 ,即
,即![]() ,
,
不妨设![]() ,则
,则![]() ,
,
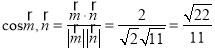 所求二面角的余弦值为
所求二面角的余弦值为![]() .
.
【点晴】
在利用线面平行的的判定定理时不仅要关注两直线直线平行而且另外两个条件(一直线在平面内,一直线在平面外)也不容忽视,大多数情况下这两个条件在作图(添加辅助线)时就可以清楚表达出,一般不需要单独证明,但也不能想当然,要仔细观察,再得出结论.

 阅读快车系列答案
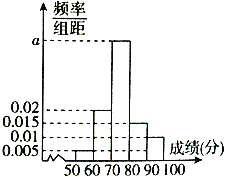
阅读快车系列答案【题目】为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示.成绩落在[70,80)中的人数为20.
男生 | 女生 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(Ⅰ)求a和n的值;
(Ⅱ)根据样本估计总体的思想,估计该校高二学生物理成绩的平均数![]() 和中位数m;
和中位数m;
(Ⅲ)成绩在80分以上(含80分)为优秀,样本中成绩落在[50,80)中的男、女生人数比为1:2,成绩落在[80,100]中的男、女生人数比为3:2,完成2×2列联表,并判断是否有95%的把握认为物理成绩优秀与性别有关.
参考公式和数据:K2=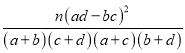 .
.
P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
k | 0.455 | 3.841 | 5.024 | 7.879 |
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
商店名称 | A | B | C | D | E |
销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
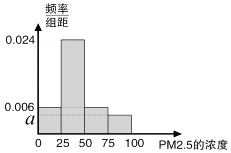
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表
组别 | PM2.5浓度 | 频数(天) | 频率 |
第一组 | (0,25] | 3 | 0.15 |
第二组 | (25,50] | 12 | 0.6 |
第三组 | (50,75] | 3 | 0.15 |
第四组 | (75,100] | 2 | 0.1 |
(1)从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(2)将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图. ①求图中a的值;
②求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.