题目内容
8.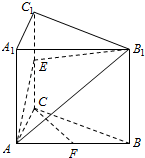 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.(Ⅰ)求证:CF⊥平面ABB1;
(Ⅱ)试确定点E的位置,使得CF∥面AEB1.
分析 (Ⅰ)利用条件推出BB1⊥平面ABC.得到CF⊥BB1.CF⊥AB.然后利用直线与平面垂直的判定定理证明CF⊥平面ABB1.
(Ⅱ)判断点E为CC1的中点,证明:取A1B1的中点,记为M.连接FM,MC1.设AB1∩FM=N,说明四边形CC1MF是平行四边形,推出N是MF的中点,得到E是CC1的中点.
解答 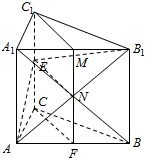 (Ⅰ)证明:∵三棱柱ABC-A1B1C1是直棱柱,∴BB1⊥平面ABC.
(Ⅰ)证明:∵三棱柱ABC-A1B1C1是直棱柱,∴BB1⊥平面ABC.
又∵CF?平面ABC,∴CF⊥BB1.
∵∠ACB=90°,AC=BC=2,F是AB中点,∴CF⊥AB.又∵BB1∩AB=B,∴CF⊥平面ABB1.…(6分)
(Ⅱ)点E为CC1的中点,证明如下:
取A1B1的中点,记为M.连接FM,MC1.设AB1∩FM=N,
∵FM∥CC1,且FM=CC1,
∴四边形CC1MF是平行四边形,
∵CF∥面AEB1,CF?面CC1MF,面CC1MF∩面AEB1=EN,
∴CF∥EN,
∵N是MF的中点,
∴E是CC1的中点.…(12分)
点评 本题考查直线与平面垂直的判定定理,直线与平面平行的判定定理的应用,考逻辑推理能力.

练习册系列答案
相关题目
3.若某公司从四位大学毕业生甲、乙、丙、丁中录用两人,这四人被录用的机会均等,则甲被录用的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
13.如图的框图表示的算法的功能是( )
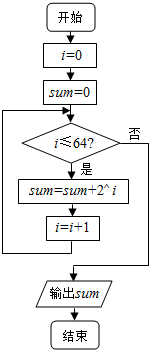

| A. | 求和S=2+22+…+264 | B. | 求和S=1+2+22+…+263 | ||
| C. | 求和S=1+2+22+…+264 | D. | 以上均不对 |
17.函数f(x)=2x-sinx在(-∞,+∞)上( )
| A. | 是增函数 | B. | 是减函数 | C. | 有最大值 | D. | 有最小值 |
 B、
B、 C、
C、 D、
D、
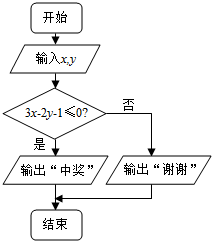 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、200人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取10人在前排就坐,其中高二代表队有5人.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、200人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取10人在前排就坐,其中高二代表队有5人.