题目内容
19.已知函数f(x)=2(a+1)lnx-ax,g(x)=$\frac{1}{2}{x^2}$-x(1)若函数f(x)在定义域内为单调函数,求实数a的取值范围;
(2)证明:若-1<a<7,则对于任意x1,x2∈(1,+∞),x1≠x2,有$\frac{{f({x_1})-f({x_2})}}{{g({x_1})-g({x_2})}}$>-1.
分析 (1)先求出函数的定义域和f′(x),将条件利用导数与函数的单调性的关系,转化成f′(x)≥0或f′(x)≤0在(0,+∞)上恒成立,对a分类讨论,分别根据一次函数的图象与性质,求出实数a的取值范围;
(2)利用二次函数的单调性判断出g(x)的单调性,不妨设x1>x2把结论进行等价转化,变形构造恰当的函数h(x),求出h′(x)并根据a的范围判断出h′(x)的符号,得到函数h(x)的单调性,即可证明结论.
解答 解:(1)函数f(x)=2(a+1)lnx-ax的定义域是(0,+∞),
∴$f′(x)=\frac{2(a+1)}{x}-a$=$\frac{-ax+2(a+1)}{x}$,
∵函数f(x)在定义域内为单调函数,
∴f′(x)≥0或f′(x)≤0在(0,+∞)上恒成立,
则-ax+2(a+1)≥0或-ax+2(a+1)≤0在(0,+∞)上恒成立,
①当a=0时,则有2≥0恒成立,函数f(x)在(0,+∞)上为增函数;
②当a>0时,函数y=-ax+2(a+1)在(0,+∞)上为减函数,
∴只要2(a+1)≤0,即a≤-1时满足f′(x)≤0成立,此时a无解;
③当a<0时,函数y=-ax+2(a+1)在(0,+∞)上为增函数,
∴只要2(a+1)≥0,即a≥-1时满足f′(x)≥0成立,此时-1≤a<0;
综上可得,实数a的取值范围是[-1,0];
证明:(2)g(x)=$\frac{1}{2}{x^2}$-x=$\frac{1}{2}(x-1)^{2}-\frac{1}{2}$在(1,+∞)单调递增,
∵x1,x2∈(1,+∞),不妨设x1>x2,∴g(x1)>g(x2),
∴$\frac{f({x}_{1})-f({x}_{2})}{g({x}_{1})-g({x}_{2})}>-1$等价于f(x1)-f(x2)>-g(x1)+g(x2),
则f(x1)+g(x1)>f(x2)+g(x2),
设h(x)=f(x)+g(x)=2(a+1)lnx-(a+1)x+$\frac{1}{2}{x^2}$,
则h′(x)=$\frac{2(a+1)}{x}-a-1+x$=$\frac{2(a+1)}{x}+x-(a+1)$,
∵-1<a<7,∴a+1>0,
∴$\frac{2(a+1)}{x}+x≥$2$\sqrt{\frac{2(a+1)}{x}•x}$=2$\sqrt{2(a+1)}$,当且仅当$\frac{2(a+1)}{x}=x$时取等号,
∴h′(x)≥2$\sqrt{2(a+1)}$-(a+1)=$2-(a+1-\sqrt{2})^{2}$,
∵-1<a<7,∴$2-(a+1-\sqrt{2})^{2}$>0,即h′(x)>0,
∴h(x)在(1,+∞)上单调递增,满足f(x1)+g(x1)>f(x2)+g(x2),
即若-1<a<7,则对于任意x1,x2∈(1,+∞),x1≠x2,有$\frac{{f({x_1})-f({x_2})}}{{g({x_1})-g({x_2})}}$>-1成立.
点评 本题考查导数与函数的单调性的关系,以及构造函数法证明不等式,考查分类讨论思想,转化思想,化简、变形能力,属于难题.

| A. | (0,+∞)上单调递减 | B. | $(\frac{1}{e},+∞)$上单调递减 | C. | $(0,\frac{1}{e})$上单调递减 | D. | (0,+∞)上单调递增 |
| A. | 60℃ | B. | 58℃ | C. | 240℃ | D. | 64℃ |
 已知圆C过点p(1,1),且与圆M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.
已知圆C过点p(1,1),且与圆M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称. 在平面内,可以用面积法证明下面的结论:从三角形内部任意一点,向各边引垂线,其长度分别为pa,pb,pc,且相应各边上的高分别为ha,hb,hc,则有$\frac{{p}_{a}}{{h}_{a}}+\frac{{p}_{b}}{{h}_{b}}+\frac{{p}_{c}}{{h}_{c}}$=1.
在平面内,可以用面积法证明下面的结论:从三角形内部任意一点,向各边引垂线,其长度分别为pa,pb,pc,且相应各边上的高分别为ha,hb,hc,则有$\frac{{p}_{a}}{{h}_{a}}+\frac{{p}_{b}}{{h}_{b}}+\frac{{p}_{c}}{{h}_{c}}$=1.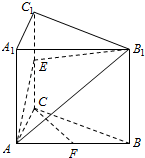 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.