题目内容
20.下列图象中,有一个是函数$f(x)=\frac{1}{3}{x^3}+a{x^2}+({a^2}-1)x+1(a∈$R,a≠0)的导函数f′(x)的图象,则f(-1)=-$\frac{1}{3}$A、
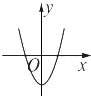 B、
B、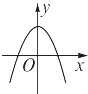 C、
C、 D、
D、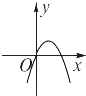
分析 求出导函数,根据导函数的二次项系数为正得到图象开口向上;利用函数解析式中有2ax,可得函数不是偶函数,得到函数的图象.再根据对称轴以及f′(0)=0求得a的值,可得f(x)的解析式,从而求得f(-1)的值.
解答 解:∵f′(x)=x2+2ax+(a2-1),∴导函数f′(x)的图象开口向上.
又∵a≠0,∴f(x)不是偶函数,其图象不关于y轴对称,
其图象必为第三张图.由图象特征知f′(0)=0,且对称轴为x=-a>0,∴a=-1,f(x)=$\frac{1}{3}$•x3-x2+1.
故f(-1)=-$\frac{1}{3}$-1+1=-$\frac{1}{3}$,
故答案为:-1.
点评 本题考查导函数的运算法则、二次函数的图象与二次函数系数的关系:开口方向与二次项系数的符号有关、对称轴公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
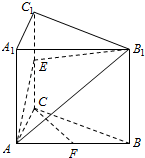 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.