题目内容
16.在△ABC中,2asinA=(2sinB-$\sqrt{3}$sinC)b+(2sinC-$\sqrt{3}$sinB)c.(1)求∠A;
(2)若a=2,b=2$\sqrt{3}$,求△ABC的面积.
分析 (1)由正弦定理可得:sinA=$\frac{a}{2R}$,sinB=$\frac{b}{2R}$,sinC=$\frac{c}{2R}$,代入已知等式整理可得:a2=b2+c2-$\sqrt{3}$bc,结合余弦定理可得cosA的值,结合范围0<A<π,
即可求得A的值.
(2)由正弦定理可得sinB,结合B范围解得B,由三角形内角和定理可求C的值,利用三角形面积公式即可得解.
解答 解:(1)∵由正弦定理可得:sinA=$\frac{a}{2R}$,sinB=$\frac{b}{2R}$,sinC=$\frac{c}{2R}$,
∴2asinA=(2sinB-$\sqrt{3}$sinC)b+(2sinC-$\sqrt{3}$sinB)c.
⇒2a$\frac{a}{2R}$=(2$\frac{b}{2R}$-$\sqrt{3}$$\frac{c}{2R}$)b+(2$\frac{c}{2R}$-$\sqrt{3}$$\frac{b}{2R}$)c.
⇒a2=b2+c2-$\sqrt{3}$bc.
∴结合余弦定理:a2=b2+c2-2bccosA,可得:cosA=$\frac{\sqrt{3}}{2}$,
∵0<A<π,
∴解得:A=$\frac{π}{6}$.
(2)∵a=2,b=2$\sqrt{3}$,A=$\frac{π}{6}$.
∴由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{2\sqrt{3}×\frac{1}{2}}{2}$=$\frac{\sqrt{3}}{2}$.
∴解得:B=$\frac{π}{3}$或$\frac{2π}{3}$,C=π-A-B=$\frac{π}{2}$或$\frac{π}{6}$.
∴S△ABC=$\frac{1}{2}$absinC=2$\sqrt{3}$或$\sqrt{3}$.
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式等知识的应用,属于基本知识的考查.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案| A. | 60℃ | B. | 58℃ | C. | 240℃ | D. | 64℃ |
 已知圆C过点p(1,1),且与圆M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.
已知圆C过点p(1,1),且与圆M:(x+2)2+(y+2)2=r2(r>0)关于直线x+y+2=0对称.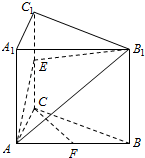 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.