题目内容
18. 某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、200人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取10人在前排就坐,其中高二代表队有5人.
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、200人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取10人在前排就坐,其中高二代表队有5人.(1)求n的值;
(2)随机从前排就坐的高一和高三两代表队中抽取3人上台抽奖,求前排同一年级代表队都被抽中的概率;
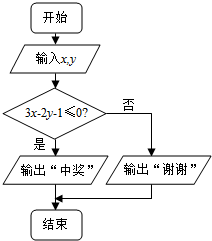
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x、y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表队中奖;若电脑显示“谢谢”,则不中奖,求该代表队中奖的概率.
分析 (1)根据分层抽样可得$\frac{5}{200}=\frac{10}{100+120+n}$,故可求n的值;
(2)求出高二代表队6人,从中抽取2人上台抽奖的基本事件,确定a和b至少有一人上台抽奖的基本事件,根据古典概型的概率公式,可得a和b至少有一人上台抽奖的概率;
(3)确定满足0≤x≤1,0≤y≤1点的区域,由条件$\left\{\begin{array}{l}{3x-2y-1≤0}\\{0≤x≤1}\\{0≤y≤1}\end{array}\right.$得到的区域为图中的阴影部分,计算面积,可求该代表中奖的概率
解答 解:(1)由题意可得$\frac{5}{200}=\frac{10}{100+120+n}$,∴n=80;
(2)前排高一共有120×$\frac{5}{200}$=3,高三共有10-=3-5=2人,记高一3人为A,B,C,高三2人为a,b,从前排就坐的高一和高三两代表队中抽取3人上台抽奖的所有基本事件有:ABC,ABa,ABb,ACa,ACb,Aab,BCa,BCb,Bab,Cab共有10个,并且是等可能的,设前排同一年级代表队都被抽中为事件M,其中事件M包含基本事件为ABC,Aab,Bab,Cab共有4种,则P(M)=$\frac{4}{10}=\frac{2}{5}$.
(3)由已知0≤x≤1,0≤y≤1,点(x,y)在如图所示的正方形OABC内,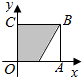
由条件$\left\{\begin{array}{l}{3x-2y-1≤0}\\{0≤x≤1}\\{0≤y≤1}\end{array}\right.$得到的区域为图中的阴影部分
由3x-2y-1=0,令y=0可得x=$\frac{1}{3}$,令y=1可得x=1
∴在x,y∈[0,1]时满足3x-2y-1≤0的区域的面积为S阴=1$-\frac{1}{2}×(1-\frac{1}{3})×1=\frac{2}{3}$
∴该代表中奖的概率为$\frac{\frac{2}{3}}{1}=\frac{2}{3}$.
点评 本题考查概率与统计知识,考查程序框图、分层抽样、概率、线性规划的计算,确定程序框图解决的问题、概率的类型是关键.

| A. | 14 | B. | 15 | C. | 16 | D. | 23 |
| A. | ∅ | B. | {x∈Z|x≥3} | C. | {3,4} | D. | {1,2} |
| A. | -3或1 | B. | 1或3 | C. | -1或-3 | D. | -1或3 |
 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB中点,AC=BC=2,AA1=4.