题目内容
在数列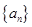 中,
中,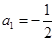 ,
,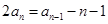
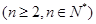 ,设
,设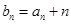 .
.
(1)证明:数列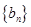 是等比数列;
是等比数列;
(2)求数列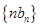 的前
的前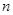 项和
项和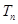 ;
;
(3)若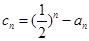 ,
,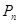 为数列
为数列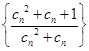 的前
的前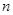 项和,求不超过
项和,求不超过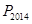 的最大的整数.
的最大的整数.
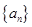 中,
中,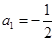 ,
,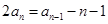
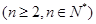 ,设
,设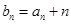 .
.(1)证明:数列
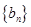 是等比数列;
是等比数列;(2)求数列
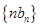 的前
的前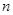 项和
项和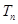 ;
;(3)若
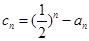 ,
,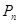 为数列
为数列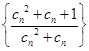 的前
的前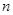 项和,求不超过
项和,求不超过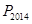 的最大的整数.
的最大的整数.(1)见解析;(2)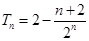 ;(3)不超过
;(3)不超过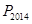 的最大的整数是
的最大的整数是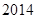 .
.
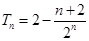 ;(3)不超过
;(3)不超过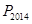 的最大的整数是
的最大的整数是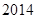 .
.试题分析:(1)注意从
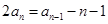 出发,得到
出发,得到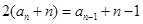 2分
2分即
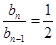 ,肯定数列
,肯定数列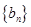 是公比为
是公比为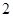 的等比数列.
的等比数列.(2)利用“错位相减法”求和.
(3)由(1)得
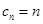 ,从而可得到
,从而可得到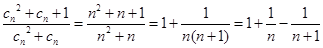 ,利用“裂项相消法”求
,利用“裂项相消法”求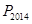 .
.利用
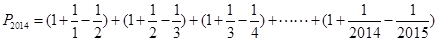
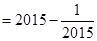 ,
,得出结论.
试题解析:(1)由
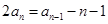 两边加
两边加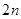 得,
得,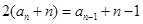 2分
2分所以
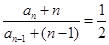 , 即
, 即 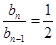 ,数列
,数列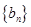 是公比为
是公比为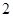 的等比数列 3分
的等比数列 3分其首项为
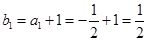 ,所以
,所以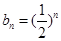 4分
4分(2)
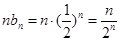 5分
5分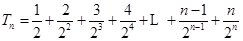 ①
①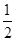
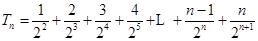 ②
②①-②得
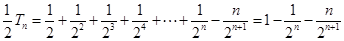
所以
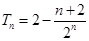 8分
8分(3)由(1)得
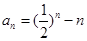 ,所以
,所以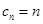
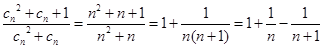 10分
10分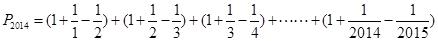
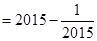
所以不超过
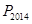 的最大的整数是
的最大的整数是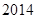 . 12分
. 12分
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
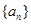 ,其前
,其前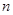 项和
项和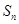 满足
满足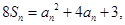 且
且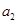 是
是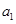 和
和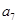 的等比中项.
的等比中项.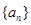 的通项公式;
的通项公式;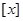 表示不超过实数
表示不超过实数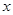 的最大整数,记
的最大整数,记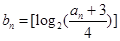 ,求
,求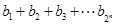 .
. bn=1.
bn=1.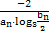 ,{cn}的前n项和为Tn,若Tn<
,{cn}的前n项和为Tn,若Tn<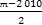 对一切n∈N*都成立,求最小正整数m.
对一切n∈N*都成立,求最小正整数m.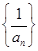 的前5项和为( )
的前5项和为( )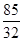
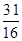
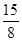
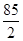
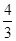 ,则{an}的前10项和等于( )
,则{an}的前10项和等于( )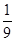 (1-310)
(1-310)