题目内容
11.若f(x)=2cos2x+$\sqrt{3}$sin2x+a(a为常数)在[0,$\frac{π}{2}$]上的最小值为-3,则a的值为( )| A. | 4 | B. | -3 | C. | -4 | D. | -6 |
分析 直接结合三角恒等变换公式化简,然后,结合[0,$\frac{π}{2}$]求得2x+$\frac{π}{6}$的范围,借助于三角函数的单调性确定sin(2x+$\frac{π}{6}$)的最小值,得2×$(-\frac{1}{2})+a+1$=-3,即可解得a的值.
解答 解:∵函数f(x)=2cos2x+$\sqrt{3}$sin2x+a=cos2x+$\sqrt{3}$sin2x+a+1=2sin(2x+$\frac{π}{6}$)+a+1,
∵x∈[0,$\frac{π}{2}$],
∴2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
∴sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],
∴f(x)min=2×$(-\frac{1}{2})+a+1$=-3,
∴解得:a=-3.
故选:B.
点评 本题重点考查了三角恒等变换公式、三角函数的图象与性质等知识,属于中档题.

练习册系列答案
相关题目
1.已知a、b为异面直线,若c∥a,则c与b的位置关系是( )
| A. | 相交 | B. | 异面 | C. | 平行 | D. | 相交或异面. |
2.计算i2=( )
| A. | 2 | B. | 0 | C. | -1 | D. | -2 |
6.在△ABC中,a2-b2-c2-bc=0,则A等于( )
| A. | 60° | B. | 45° | C. | 120° | D. | 30° |
1.与函数y=x有相同图象的一个函数是( )
| A. | y=$\frac{{x}^{3}}{{x}^{2}}$ | B. | y=a${\;}^{lo{g}_{a}x}$ | C. | y=$\sqrt{{x}^{2}}$ | D. | y=logaax |
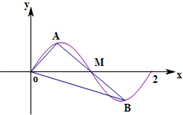 如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )
如图,过点M(1,0)的直线与函数y=sinπx(0≤x≤2)的图象交于A,B两点,则$\overrightarrow{OM}$•($\overrightarrow{OA}$+$\overrightarrow{OB}$)等于( )