题目内容
3．已知Z1=2+i，Z2=$\frac{{{Z_1}+i}}{{（2i+1）-{Z_1}}}$，求$\overline{Z_1}$，|Z1|，Z2．分析 根据共轭复数的定义和复数模的公式求出$\overline{Z_1}$、|Z1|，由复数代数形式的乘除运算化简Z2．
解答 解：由题意知，Z1=2+i，
∴$\overline{Z_1}$=2-i，$|{Z_1}|=\sqrt{{2^2}+{1^2}}=\sqrt{5}$，
${Z_2}=\frac{{{Z_1}+i}}{{（2i+1）-{Z_1}}}$=$\frac{2+i+i}{（2i+1）-（2+i）}=\frac{2+2i}{-1+i}=\frac{2（1+i）（-1-i）}{（-1+i）（-1-i）}=-2i$．
点评 本题考查复数代数形式的乘除运算，共轭复数和复数相等的定义，以及化简、计算能力．
练习册系列答案
相关题目
如图，小正六边形沿着大正六边形的边，按顺时针方向滚动，小正六边形的边长是大正六边形边长的一半．当小正六边形沿着大正六边形的边滚动4周后返回出发时的位置，记在这个过程中向量$\overrightarrow{OA}$围绕着点O旋转θ角（其中O为小正六边形的中心），则sin$\frac{θ}{36}$等于-$\frac{\sqrt{3}}{2}$．
8．
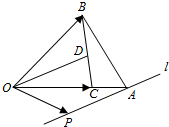在△OAB中，C为OA上的一点，且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$，D是BC的中点，过点A的直线l∥OD，P是直线l上的动点，若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$，则λ1-λ2=（ ）
在△OAB中，C为OA上的一点，且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$，D是BC的中点，过点A的直线l∥OD，P是直线l上的动点，若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$，则λ1-λ2=（ ）| A． | $\frac{3}{2}$ | B． | -$\frac{3}{2}$ | C． | $\frac{5}{4}$ | D． | -$\frac{5}{4}$ |