题目内容
20.若函数f(x)=log0.5(5x2-ax+8)在[-1,+∞)上为减函数,则实数a的取值范围为(-13,-10].分析 先根据复合函数的单调性确定函数g(x)在[-1,+∞)上是增函数,再根据对数函数的真数大于0可得答案
解答 解:设g(x)=5x2-ax+8,
∵函数f(x)=log0.5(5x2-ax+8)在[-1,+∞)上为减函数,y=log0.5x在(0,+∞)上为减函数,
故函数g(x)在[-1,+∞)上是增函数,且恒为正,
即$\left\{\begin{array}{l}\frac{a}{10}≤-1\\ g(-1)=13+a>0\end{array}\right.$,
解得-13<a≤-10.
故答案为:(-13,-10]
点评 本题主要考查复合函数的运算性质,即同增异减的性质,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.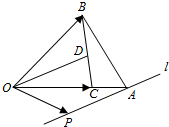 在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
 在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |
10.已知数列{an}的前n项和为Sn,若an=$\frac{1}{{\sqrt{n}+\sqrt{n+1}}}$,Sn=10,则n=( )
| A. | 90 | B. | 121 | C. | 119 | D. | 120 |