题目内容

【题目】设定义在R上的奇函数f（x）在（0，+∞）上为增函数，且f（2）=0，则不等式f（x）＜0的解集为 ．

【答案】（﹣∞，﹣2）∪（0，2）
【解析】解：如图所示，不等式f（x）＜0的解集为
（﹣∞，﹣2）∪（0，2）．
所以答案是：（﹣∞，﹣2）∪（0，2）．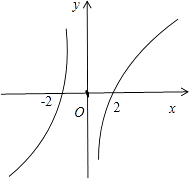

【考点精析】利用函数单调性的性质和函数奇偶性的性质对题目进行判断即可得到答案，需要熟知函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集；在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇．

练习册系列答案
相关题目

【题目】已知函数f（x）= （m，n为常数）是定义在[﹣1，1]上的奇函数，且f（﹣1）=﹣ ．
（1）求函数f（x）的解析式；
（2）解关于x的不等式f（2x﹣1）＜﹣f（x）．

【题目】已知幂函数f（x）=（﹣2m2+m+2）xm+1为偶函数．
（1）求f（x）的解析式；
（2）若函数y=f（x）﹣2（a﹣1）x+1在区间（2，3）上为单调函数，求实数a的取值范围．

【题目】已知函数f（x）=|lgx|．若a≠b且，f（a）=f（b），则a+b的取值范围是（ ）
A.（1，+∞）
B.[1，+∞）
C.（2，+∞）
D.[2，+∞）

【题目】如图，四棱锥中， ⊥底面， ， 为上一点．

（1）证明： ∥平面；

若， ，求二面角的正弦值．

【题目】（1）请根据对数函数来指出函数的基本性质（结论不要求证明），并画出图像；

（2）拉普拉斯称赞对数是一项“使天文学家寿命倍増”的发明.对数可以将大数之间的乘除运算简化为加减运算，请证明： ；

（3）2017年5月23日至27日，围棋世界冠军柯洁与DeepMind公司开发的程序“AlphaGo”进行三局人机对弈，以复杂的围棋来测试人工智能.围棋复杂度的上限约为，而根据有关资料，可观测宇宙中普通物质的原子总数约为.甲、乙两个同学都估算了的近似值，甲认为是,乙认为是.现有两种定义：

①若实数满足，则称比接近；

②若实数，且，满足，则称比接近；请你任选取其中一种定义来判断哪个同学的近似值更接近，并说明理由.

【题目】已知y=f（x）（x∈R）是偶函数，当x≥0时，f（x）=x2﹣2x．
（1）求f（x）的解析式；
（2）若不等式f（x）≥mx在1≤x≤2时都成立，求m的取值范围．

【题目】如图，在棱长为3的正方体ABCD﹣A1B1C1D1中，A1E=CF=1．

（1）求两条异面直线AC1与D1E所成角的余弦值；
（2）求直线AC1与平面BED1F所成角的正弦值．

【题目】若函数f（x）= 无最大值，则实数a的取值范围 ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网