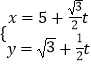��Ŀ����
����Ŀ����1������ݶ�������![]() ��ָ������
��ָ������![]() �Ļ������ʣ����۲�Ҫ��֤������������ͼ��
�Ļ������ʣ����۲�Ҫ��֤������������ͼ��
��2��������˹��������һ�ʹ����ѧ�������������ķ���.�������Խ�����֮��ij˳������Ϊ�Ӽ����㣬��֤���� ![]() ��
��
��3��2017��5��23����27�գ�Χ������ھ��½���DeepMind��˾�����ij�����AlphaGo�����������˻����ģ��Ը��ӵ�Χ���������˹�����.Χ�帴�Ӷȵ�����ԼΪ![]() ���������й����ϣ��ɹ۲���������ͨ���ʵ�ԭ������ԼΪ
���������й����ϣ��ɹ۲���������ͨ���ʵ�ԭ������ԼΪ![]() .�ס�������ͬѧ��������
.�ס�������ͬѧ��������![]() �Ľ���ֵ������Ϊ��
�Ľ���ֵ������Ϊ��![]() ,����Ϊ��
,����Ϊ��![]() .�������ֶ��壺
.�������ֶ��壺
����ʵ��![]() ����
����![]() �����
�����![]() ��
��![]() �ӽ�
�ӽ�![]() ��
��
����ʵ��![]() ����
����![]() ������
������![]() �����
�����![]() ��
��![]() �ӽ�
�ӽ�![]() ��������ѡȡ����һ�ֶ������ж��ĸ�ͬѧ�Ľ���ֵ���ӽ�
��������ѡȡ����һ�ֶ������ж��ĸ�ͬѧ�Ľ���ֵ���ӽ�![]() ����˵������.
����˵������.
���𰸡�(1)������;(2) ����������3��������.
�������������������1�����ݶ������������ʼ�����������![]() �Ļ������ʣ�
�Ļ������ʣ�
��2����![]() ����
����![]() ������ʵ��ָ���ݵ����㣬��������֤����
������ʵ��ָ���ݵ����㣬��������֤����
��3���ֱ���ö��壬����ָ���ݺͶ��������㣬������������.
���������
(1) ![]() ��
��
��������Ϊ�������� ![]() ��ֵ��
��ֵ�� ![]() ������������
������������![]() ��
��![]()
(�ж���ż�ԡ������Բ������)
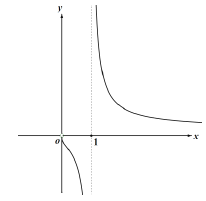
��2��֤���� ��![]()
![]()
��![]() ֤�����
֤�����
��3�����ö��壨��: ![]()
![]()
��![]()
![]()
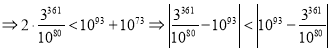
���Լ�ͬѧ�Ľ���ֵ���ӽ�![]()
���ö��壨��
![]()
�Ĺ�ֵ ![]() ���ҵĹ�ֵ
���ҵĹ�ֵ![]()
��Ϊ![]() ��
��
������ͬѧ�Ľ���ֵ���ӽ�![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�