题目内容
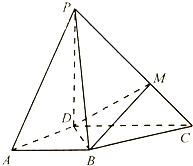
【题目】如图,四棱锥![]() 中,
中, ![]() ⊥底面
⊥底面![]() ,
, ![]() ,
, ![]()
![]() 为
为![]() 上一点
上一点![]() .
.
(1)证明: ![]() ∥平面
∥平面![]() ;
;
若![]() ,
, ![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)在![]() 上取点
上取点![]() ,使
,使![]() ,根据平几知识得四边形
,根据平几知识得四边形![]() 是平行四边形,即得
是平行四边形,即得![]() ,最后根据线面平行判定定理证得
,最后根据线面平行判定定理证得![]() ∥平面
∥平面![]() (2)利用空间向量求二面角,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组求各面法向量,根据向量数量积求两法向量夹角,最后根据二面角与法向量夹角关系得结果
(2)利用空间向量求二面角,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组求各面法向量,根据向量数量积求两法向量夹角,最后根据二面角与法向量夹角关系得结果
试题解析:证明:(1)在![]() 上取点
上取点![]() ,使
,使![]() ,
,
则![]() ,
, ![]() ,
,
则四边形![]() 是平行四边形,则
是平行四边形,则![]() ,
,
![]()
![]()
则平面![]() ∥平面
∥平面![]() ,∵
,∵![]()
![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]()
(2)![]() 是正三角形,建立以
是正三角形,建立以![]() 为坐标原点的空间直角坐标系如图:
为坐标原点的空间直角坐标系如图:
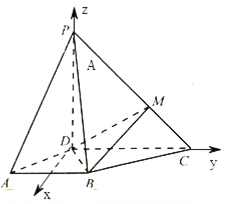
则![]()
所以![]()
设平面![]() 的法向量为
的法向量为![]()
则由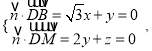 得
得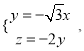 令
令![]() 则
则![]() ,
,
则![]()
同理得平面![]() 的法向量为
的法向量为![]()
则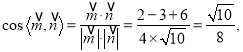
则二面角![]() 的正弦值
的正弦值![]()

【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位: ![]() )有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量![]() (单位:瓶)的分布列;
(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元).当六月份这种酸奶一天的进货量(单位:瓶)为多少时,
(单位:元).当六月份这种酸奶一天的进货量(单位:瓶)为多少时, ![]() 的数学期望达到最大值?
的数学期望达到最大值?
【题目】某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
分数段 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
男 | 3 | 9 | 18 | 15 | 6 | 9 |
女 | 6 | 4 | 5 | 10 | 13 | 2 |
(I)估计男、女生各自的平均分(同一组数据用该组区间中点值作代表),从计算结果看,能否判断数学成绩与性别有关;
(II)规定80分以上为优分(含80分),请你根据已知条件完成2×2列联表,并判断是否有90%以上的把握认为“数学成绩与性别有关”. ( ,其中
,其中![]() )
)
