题目内容
【题目】已知函数f(x)= ![]() (m,n为常数)是定义在[﹣1,1]上的奇函数,且f(﹣1)=﹣
(m,n为常数)是定义在[﹣1,1]上的奇函数,且f(﹣1)=﹣ ![]() .
.
(1)求函数f(x)的解析式;
(2)解关于x的不等式f(2x﹣1)<﹣f(x).
【答案】
(1)解:由于函数f(x)= ![]() (m,n为常数)是定义在[﹣1,1]上的奇函数,
(m,n为常数)是定义在[﹣1,1]上的奇函数,
∴f(0)= ![]() =0,∴n=0,
=0,∴n=0,
再根据f(﹣1)= ![]() =﹣
=﹣ ![]() ,∴m=1,
,∴m=1,
∴f(x)= ![]() =
= ![]()
(2)解:关于x的不等式f(2x﹣1)<﹣f(x)=﹣f(x),
∵f(x)= ![]() 在(0,1]上单调递增,∴f(x)在[﹣1,1]上单调递增.
在(0,1]上单调递增,∴f(x)在[﹣1,1]上单调递增.
故由不等式可得 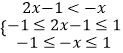 ,求得0≤x<
,求得0≤x< ![]() ,
,
故不等式的解集为{x|0≤x< ![]() }
}
【解析】(1)由f(0)= ![]() =0,求得n=0,再根据f(﹣1)=﹣
=0,求得n=0,再根据f(﹣1)=﹣ ![]() ,求得m=1,∴f(x)得解析式.(2)关于x的不等式即f(2x﹣1)<﹣f(x),再根据f(x)在[﹣1,1]上单调递增,可得不等式组
,求得m=1,∴f(x)得解析式.(2)关于x的不等式即f(2x﹣1)<﹣f(x),再根据f(x)在[﹣1,1]上单调递增,可得不等式组 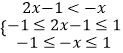 ,由此求得x的范围.
,由此求得x的范围.
【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件) | 产品B(件) | ||
研制成本、搭载费用之和(万元) | 20 | 30 | 计划最大资金额300万元 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位: ![]() )有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 |
|
|
|
|
|
|
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量![]() (单位:瓶)的分布列;
(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元).当六月份这种酸奶一天的进货量(单位:瓶)为多少时,
(单位:元).当六月份这种酸奶一天的进货量(单位:瓶)为多少时, ![]() 的数学期望达到最大值?
的数学期望达到最大值?