题目内容
【题目】如图，在棱长为3的正方体ABCD﹣A1B1C1D1中，A1E=CF=1．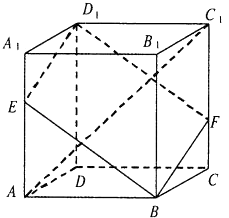 
（1）求两条异面直线AC1与D1E所成角的余弦值；
（2）求直线AC1与平面BED1F所成角的正弦值．
【答案】
（1）解：以D为原点，建立空间直角坐标系D﹣xyz如图所示：
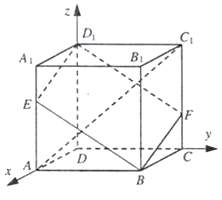
则A（3，0，0），C1=（0，3，3），D1=（0，0，3），E（3，0，2）
∴ 
=（﹣3，3，3）， 
=（3，0，﹣1）
∴cosθ=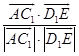 
= 
=﹣ 
则两条异面直线AC1与D1E所成角的余弦值为
（2）解：B（3，3，0）， 
=（0，﹣3，2）， =（3，0，﹣1）
设平面BED1F的一个法向量为 
=（x，y，z）
由 
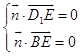得 
令x=1，则 =（1，2，3）
则直线AC1与平面BED1F所成角的正弦值为
| 
|= 
= 
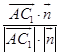【解析】（1）以以D为原点，建立空间直角坐标系D﹣xyz，则我们易求出已知中，各点的坐标，进而求出向量 ， 的坐标．代入向量夹角公式，结合异面直线夹角公式，即可得到答案．（2）设出平面BED1F的一个法向量为 ，根据法向量与平面内任一向量垂直，数量积为0，构造方程组，求出平面BED1F的法向量为 的坐标，代入线面夹角向量公式，即可求出答案．
【考点精析】根据题目的已知条件，利用异面直线及其所成的角和空间角的异面直线所成的角的相关知识可以得到问题的答案，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系；已知
为两异面直线，A，C与B，D分别是上的任意两点，所成的角为
，则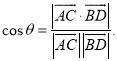
．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
