题目内容
【题目】已知圆C经过点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上,又直线
上,又直线![]() 与圆C交于P,Q两点.
与圆C交于P,Q两点.
(1)求圆C的方程;
(2)若![]() ,求实数
,求实数![]() 的值;
的值;
(3)过点![]() 作直线
作直线![]() ,且
,且![]() 交圆C于M,N两点,求四边形
交圆C于M,N两点,求四边形![]() 的面积的最大值.
的面积的最大值.
【答案】(1)x 2 +y 2 =4(2)k=0(3)7
【解析】试题分析:(1)设圆心为![]() ,半径为
,半径为![]() .故
.故![]() ,建立方程,从而可求圆
,建立方程,从而可求圆![]() 的方程;(2)利用向量的数量积公式,求得
的方程;(2)利用向量的数量积公式,求得![]() ,计算圆心到直线
,计算圆心到直线![]() 的距离
的距离![]() ,即可求解实数
,即可求解实数![]() 的值;(3)方法1、设圆
的值;(3)方法1、设圆![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,求得
,求得![]() ,根据垂径定理和勾股定理,可得
,根据垂径定理和勾股定理,可得![]() ,在利用基本不等式,可求四边形
,在利用基本不等式,可求四边形![]() 面积的最大值;方法2、利用弦长公式
面积的最大值;方法2、利用弦长公式![]() ,
, 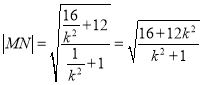 ,表示三角形的面积,在利用基本不等式,可求四边形
,表示三角形的面积,在利用基本不等式,可求四边形![]() 面积的最大值.
面积的最大值.
试题解析:(1)设圆心为![]() ,半径为
,半径为![]() .故
.故![]() ,易得
,易得![]() ,
,
因此圆的方程为![]() .
.
(2)因为![]() ,且
,且![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
故![]() ,
, ![]() ,所以
,所以![]() 到直线
到直线![]() 的距离
的距离![]() ,又
,又![]() ,所以
,所以![]() .
.
又解:设P![]() ,
, ![]() ,则
,则![]() ,即
,即![]() ,
,
由![]() 得
得![]() ,∴
,∴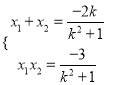 ,
,
代入![]() 得
得![]() ,∴
,∴![]() ;
;
(3)设圆心![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() .
.
因为直线![]() 都经过点
都经过点![]() ,且
,且![]() ,根据勾股定理,有
,根据勾股定理,有![]() ,
,
又![]() ,
,
故![]()
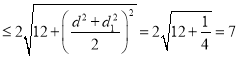 当且仅当
当且仅当![]() 时,等号成立,所以
时,等号成立,所以![]() .
.
(3)又解:由已知![]() ,由(2)的又解可得
,由(2)的又解可得![]() ,
,
同理可得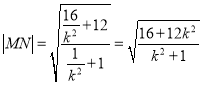 ,
,
∴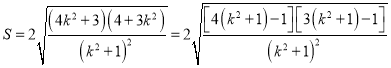
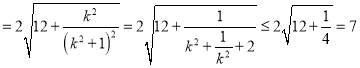 ,
,
当且仅当![]() 时等号成立,所以
时等号成立,所以![]() .
.

练习册系列答案
相关题目