题目内容
【题目】已知函数f(x)=![]() (x﹣2)的定义域为集合A,函数
(x﹣2)的定义域为集合A,函数![]() 的值域为集合B.
的值域为集合B.
(1)求A∪B;
(2)若集合C={x|a≤x≤3a﹣1},且B∩C=C,求实数a的取值范围.
【答案】解(1)函数f(x)的自变量x需满足条件![]() ,
,
解得,2<x≤4,所以,A={x|2<x≤4},
对于函数g(x),因为![]() ≤x≤8,
≤x≤8,
所以,g(x)=log2x∈[﹣2,3],
因此,B={x|﹣2≤x≤3},
所以,A∪B={x|﹣2≤x≤4};
(2)由B∩C=C得,CB,对集合C讨论如下:
①当C=时,a>3a﹣1,解得a<![]() ,
,
因为空集是任何集合的子集,故符合题意;
②当C≠时,需要满足下列条件: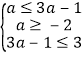 ,解得,
,解得,![]() ≤a≤
≤a≤![]() ,
,
综合以上讨论得,实数a的取值范围为:(﹣∞,![]() ].
].
【解析】(1)先求出集合A={x|2<x≤4},B={x|﹣2≤x≤3},再直接取它们的并集;
(2)问题等价为CB,再对集合C分类讨论,得出实数a的取值范围.
【考点精析】认真审题,首先需要了解集合的交集运算(交集的性质:(1)A∩B![]() A,A∩B
A,A∩B![]() B,A∩A=A,A∩
B,A∩A=A,A∩![]() =
=![]() ,A∩B=B∩A;(2)若A∩B=A,则A
,A∩B=B∩A;(2)若A∩B=A,则A![]() B,反之也成立).
B,反之也成立).

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目