ƒøƒ⁄»ð
°æƒø°øƒ≥—ß–£‘⁄“ª¥Œµ⁄∂˛øŒÃ√ªÓ∂Ø÷–£¨Ãÿ“‚…Ë÷√¡Àπ˝πÿ÷«¡¶”Œœ∑£¨”Œœ∑π≤ŒÂπÿ£ÆπÊ∂®µ⁄“ªπÿ√ªπ˝’þ√ªΩ±¿¯£¨π˝![]()
![]() πÿ’þΩ±¿¯
πÿ’þΩ±¿¯![]() º˛–°Ω±∆∑£®Ω±∆∑∂º“ª—˘£©£Æœ¬Õº «–°√˜‘⁄10¥Œπ˝πÿ”Œœ∑÷–π˝πÿ ˝µƒÃı–ŒÕº£¨“‘¥À∆µ¬ π¿º∆∏≈¬ £Æ
º˛–°Ω±∆∑£®Ω±∆∑∂º“ª—˘£©£Æœ¬Õº «–°√˜‘⁄10¥Œπ˝πÿ”Œœ∑÷–π˝πÿ ˝µƒÃı–ŒÕº£¨“‘¥À∆µ¬ π¿º∆∏≈¬ £Æ
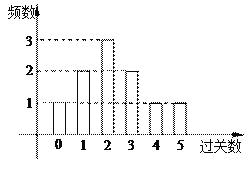
(¢Ò)π¿º∆–°√˜‘⁄1¥Œ”Œœ∑÷–À˘µ√Ω±∆∑ ˝µƒ∆⁄Õ˚÷µ£ª
(¢Ú)π¿º∆–°√˜‘⁄3 ¥Œ”Œœ∑÷–÷¡…Ÿπ˝¡Ωπÿµƒ∆Ωæ˘¥Œ ˝£ª
(¢Û)π¿º∆–°√˜‘⁄3 ¥Œ”Œœ∑÷–À˘µ√Ω±∆∑≥¨π˝30º˛µƒ∏≈¬ £Æ
°æ¥∞∏°ø£®1£©4£ª£®2£©2.1£ª£®3£©0.031
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©¡–≥ˆ–°√˜‘⁄1¥Œ”Œœ∑÷–À˘µ√Ω±∆∑ ˝Œ™![]() µƒ∑÷≤º¡–£¨∏˘æð∑÷≤º¡–«Û≥ˆ∆⁄Õ˚º¥ø…£ª£®2£©”…±Ìø…µ√–°√˜‘⁄1 ¥Œ”Œœ∑÷–÷¡…Ÿπ˝¡Ωπÿµƒ∏≈¬ Œ™0.7£¨”…∂˛œÓ∑÷≤ºø…µ√Ω·π˚£ª£®3£©∑÷Œˆø…µ√–°√˜‘⁄3 ¥Œ”Œœ∑÷–À˘µ√Ω±∆∑≥¨π˝30º˛∫¨»˝¿ý£∫«°∫√“ª¥Œ
µƒ∑÷≤º¡–£¨∏˘æð∑÷≤º¡–«Û≥ˆ∆⁄Õ˚º¥ø…£ª£®2£©”…±Ìø…µ√–°√˜‘⁄1 ¥Œ”Œœ∑÷–÷¡…Ÿπ˝¡Ωπÿµƒ∏≈¬ Œ™0.7£¨”…∂˛œÓ∑÷≤ºø…µ√Ω·π˚£ª£®3£©∑÷Œˆø…µ√–°√˜‘⁄3 ¥Œ”Œœ∑÷–À˘µ√Ω±∆∑≥¨π˝30º˛∫¨»˝¿ý£∫«°∫√“ª¥Œ![]() ∫Õ¡Ω¥Œ
∫Õ¡Ω¥Œ![]() £¨«°∫√∂˛¥Œ
£¨«°∫√∂˛¥Œ![]() £¨«°∫√»˝¥Œ
£¨«°∫√»˝¥Œ![]() £¨”…ª•≥‚ ¬º˛º∞œýª•∂¿¡¢ ¬º˛∑¢…˙µƒ∏≈¬ ø…µ√Ω·π˚.
£¨”…ª•≥‚ ¬º˛º∞œýª•∂¿¡¢ ¬º˛∑¢…˙µƒ∏≈¬ ø…µ√Ω·π˚.
‘Ã‚Ω‚Œˆ£∫ (1)…Ë–°√˜‘⁄1¥Œ”Œœ∑÷–À˘µ√Ω±∆∑ ˝Œ™![]() £¨‘Ú
£¨‘Ú![]() µƒ∑÷≤º¡–Œ™
µƒ∑÷≤º¡–Œ™
| 0 | 1 | 2 | 4 | 8 | 16 |
P | 0.1 | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 |
![]() µƒ∆⁄Õ˚÷µ
µƒ∆⁄Õ˚÷µ![]() £ª
£ª
(2)–°√˜‘⁄1 ¥Œ”Œœ∑÷–÷¡…Ÿπ˝¡Ωπÿµƒ∏≈¬ Œ™0.7£¨
…Ë–°√˜‘⁄3 ¥Œ”Œœ∑÷–÷¡…Ÿπ˝¡Ωπÿµƒ¥Œ ˝Œ™X£¨ø…÷™![]() £¨
£¨
‘ÚXµƒ∆Ωæ˘¥Œ ˝![]() £ª
£ª
(3)–°√˜‘⁄3 ¥Œ”Œœ∑÷–À˘µ√Ω±∆∑≥¨π˝30º˛∫¨»˝¿ý£∫«°∫√“ª¥Œ![]() ∫Õ¡Ω¥Œ
∫Õ¡Ω¥Œ![]() £¨«°∫√∂˛¥Œ
£¨«°∫√∂˛¥Œ![]() £¨«°∫√»˝¥Œ
£¨«°∫√»˝¥Œ![]() £¨
£¨
![]() £¨
£¨
![]() =
=![]() £¨
£¨
![]()
À˘“‘–°√˜‘⁄3 ¥Œ”Œœ∑÷–À˘µ√Ω±∆∑≥¨π˝30º˛µƒ∏≈¬ Œ™![]() £Æ
£Æ

