Question

【题目】已知函数f（x）=x2﹣2ax+2，x∈[﹣5，5]
（1）求实数a的取值范围，使y=f（x）在定义域上是单调递减函数；
（2）用g（a）表示函数y=f（x）的最小值，求g（a）的解析式．

Answer 1

【答案】解：（1）函数f（x）的对称轴为x=a；
∵f（x）在[﹣5，5]上是单调递减函数；
∴a≥5；
∴实数a的取值范围为[5，+∞）；
（2）①当a≤﹣5时，f（x）在[﹣5，5]上单调递增；
∴f（x）min=f（﹣5）=27+10a；
②当﹣5＜a＜5时，；
③当a≥5时，f（x）在[﹣5，5]上单调递减；
∴f（x）min=f（5）=27﹣10a；
∴．
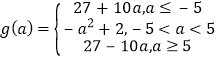【解析】（1）可求出f（x）的对称轴为x=a，而要使y=f（x）在[﹣5，5]上单调递减，则需满足a≥5，这便得到了a的取值范围；
（2）可讨论对称轴x=a和区间[﹣5，5]的关系：分a≤﹣5，﹣5＜a＜5，和a≥5三种情况，然后根据f（x）在[﹣5，5]上的单调性及取得顶点情况求出每种情况的f（x）的最小值，从而便可得出g（a）的解析式．
【考点精析】利用函数单调性的性质对题目进行判断即可得到答案，需要熟知函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集．