Question

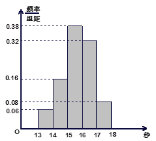
【题目】某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：第一组，第二组,…,第五组,下图是按上述分组方法得到的频率分布直方图.

(1)若成绩大于等于14秒且小于16秒为良好，求该班在这次百米测试中成绩良好的人数；

(2)若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1的概率.

Answer 1

【答案】（1）人（2）4/7

【解析】

试题（1）根据频率分步直方图做出这组数据的成绩在[14，16）内的人数为50×0.16+50×0.38，这是频率，频数和样本容量之间的关系．

（2）根据频率分步直方图做出要用的各段的人数，设出各段上的元素，用列举法写出所有的事件和满足条件的事件，根据概率公式做出概率．

解：（1）由频率分布直方图知，成绩在[14，16）内的

人数为50×0.16+50×0.38=27（人）

∴该班成绩良好的人数为27人．

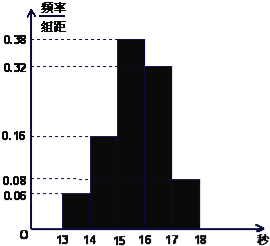
（2）由频率分布直方图知，成绩在[13，14）的人数为50×0.06=3人，

设为x，y，z

成绩在[17，18）的人数为50×0.08=4人，设为A，B，C，D

若m，n∈[13，14）时，有xy，zx，zy，3种情况；

若m，n∈[17，18）时，有AB，AC，AD，BC，BD，CD共6种情况；

若m，n分别在[13，14）和[17，18）内时，

A B C D

x xA xB xC xD

y yA yB yC yD

z zA zB zC zD

共12种情况．

∴基本事件总数为21种，事件“|m﹣n|＞1”所包含的基本事件个数有12种．

∴P（|m﹣n|＞1）=