题目内容
【题目】如图,已知四边形![]() 是矩形,
是矩形,![]() 是坐标原点,
是坐标原点,![]() 、
、![]() 、
、![]() 、
、![]() 按逆时针排列,
按逆时针排列,![]() 的坐标是
的坐标是![]() ,
,![]() .
.
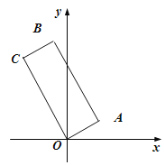
(1)求点![]() 的坐标;
的坐标;
(2)求![]() 所在直线的方程;
所在直线的方程;
(3)求![]() 的外接圆方程.
的外接圆方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意可得![]() 的斜率为
的斜率为![]() ,
,![]() 所在的直线方程为
所在的直线方程为![]() ,
,![]() ,设
,设![]() ,利用勾股定理即可得出点的坐标.
,利用勾股定理即可得出点的坐标.
(2)因为![]() 与
与![]() 平行可得OA的斜率,利用点斜式可得
平行可得OA的斜率,利用点斜式可得![]() 所在直线的方程.
所在直线的方程.
(3)由题意知![]() 的外接圆也是矩形
的外接圆也是矩形![]() 的外接圆,原问题转化为求解以线段
的外接圆,原问题转化为求解以线段![]() 为直径的圆,分别确定圆心和半径即可求得外接圆的方程.
为直径的圆,分别确定圆心和半径即可求得外接圆的方程.
(1)因为四边形![]() 是矩形,
是矩形,![]() 所在直线的斜率
所在直线的斜率![]() ,
,
∴![]() 的斜率为
的斜率为![]() ,
,![]() 所在的直线方程为
所在的直线方程为![]() ,
,
因为![]() ,设
,设![]() ,
,
则![]() ,
,
所以![]() 或
或![]() (舍去),所以点
(舍去),所以点![]() 的坐标为
的坐标为![]() .
.
(2)因为![]() 与
与![]() 平行,所以
平行,所以![]() 所在直线的斜率
所在直线的斜率![]()
所以![]() 所在直线的方程为
所在直线的方程为![]() ,即
,即![]()
(3)由题意知![]() 的外接圆也是矩形
的外接圆也是矩形![]() 的外接圆,所以线段
的外接圆,所以线段![]() 的中点即为圆心,半径
的中点即为圆心,半径![]()
因为![]() ,
,![]() ,所以圆心坐标为
,所以圆心坐标为![]()
又![]() ,所以半径
,所以半径![]()
所以![]() 外接圆的方程为
外接圆的方程为![]()

练习册系列答案
相关题目
【题目】某城镇社区为了丰富辖区内广大居民的业余文化生活,创建了社区“文化丹青”大型活动场所,配备了各种文化娱乐活动所需要的设施,让广大居民健康生活、积极向上.社区最近四年内在“文化丹青”上的投资金额统计数据如表:(为了便于计算,把2015年简记为5,其余以此类推)
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
(1)利用所给数据,求出投资金额![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该社区在2019年在“文化丹青”上的投资金额.
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ![]() .)
.)