题目内容
6.无论k为何值,直线(k+2)x+(1-k)y-4k-5=0都过一个定点,则定点坐标为(3,-1).分析 直线即即 k(x-y-4)+(2x+y-5)=0,令参数k的系数等于零,求得x和y的值,即可得到定点的坐标.
解答 解:直线(k+2)x+(1-k)y-4k-5=0,即 k(x-y-4)+(2x+y-5)=0,
它一定经过直线x-y-4=0和直线2x+y-5=0的交点M.
由$\left\{\begin{array}{l}{x-y-4=0}\\{2x+y-5=0}\end{array}\right.$ 求得$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$,故点M为(3,-1),
故答案为:(3,-1).
点评 本题主要考查直线过定点问题,令参数k的系数等于零,求得x和y的值,即可得到定点的坐标,属于基础题.

练习册系列答案
相关题目
16.已知函数f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,把函数f(x)的图象沿x轴向左平移$\frac{π}{6}$个单位,得到函数g(x)的图象.若在区间[0,π]上随机取一个数x,则事件“g(x)≥1”发生的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
14.随机变量X的分布列为
若p1,p2,p3成等差数列,则公差d的取值范围是[-$\frac{1}{3}$,$\frac{1}{3}$].
| X | x1 | x2 | x3 |
| P | p1 | p2 | p3 |
11.sin(-600°)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
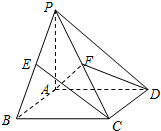 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,AD=4,E、F依次是PB、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,AD=4,E、F依次是PB、PC的中点.