题目内容
17.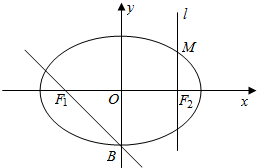 如图:在直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点分别为F1、F2.过右焦点F2与x轴垂直的直线l与椭圆C相交,其中一个交点为$M(\sqrt{2},1)$.
如图:在直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点分别为F1、F2.过右焦点F2与x轴垂直的直线l与椭圆C相交,其中一个交点为$M(\sqrt{2},1)$.(1)求椭圆C的方程;
(2)设椭圆C的一个顶点为B(0,-b),求点M到直线BF1的距离;
(3)过F1M中点的直线l1交椭圆于P、Q两点,求|PQ|长的最大值以及相应的直线方程.
分析 (1)设右焦点F2为(c,0),令x=c,代入椭圆方程,可得c=$\sqrt{2}$,$\frac{{b}^{2}}{a}$=1,解方程可得a,b,进而得到椭圆方程;
(2)求得直线BF1的方程,由点到直线的距离公式,计算即可得到所求值;
(3)过F1M中点的直线l1的方程设为x=m(y-$\frac{1}{2}$),代入椭圆方程,运用韦达定理和弦长公式,化简整理即可得到弦长的取值范围,再由斜率为0,求得直线方程,代入椭圆方程,求得PQ的长,即可得到最大值.
解答 解:(1)设右焦点F2为(c,0),
令x=c,代入椭圆可得y=±b$\sqrt{1-\frac{{c}^{2}}{{a}^{2}}}$,
由M($\sqrt{2}$,1),即有c=$\sqrt{2}$,$\frac{{b}^{2}}{a}$=1,
又a2-b2=2,解得a=2,b=$\sqrt{2}$,
则椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1;
(2)由题意可得B(0,-$\sqrt{2}$),F1(-$\sqrt{2}$,0),
直线BF1的方程为x+y+$\sqrt{2}$=0,
则点M到直线BF1的距离为$\frac{|\sqrt{2}+1+\sqrt{2}|}{\sqrt{2}}$=2+$\frac{\sqrt{2}}{2}$;
(3)过F1M中点的直线l1的方程设为x=m(y-$\frac{1}{2}$),
代入椭圆方程,可得(2+m2)y2-m2y+$\frac{1}{4}$m2-4=0,
由于中点(0,$\frac{1}{2}$)在椭圆内,故直线与椭圆相交,
设交点P(x1,y1),Q(x2,y2),
即有y1+y2=$\frac{{m}^{2}}{2+{m}^{2}}$,y1y2=$\frac{{m}^{2}-16}{4(2+{m}^{2})}$,
弦长|PQ|=$\sqrt{1+{m}^{2}}$•|y1-y2|=$\sqrt{1+{m}^{2}}$•$\sqrt{(\frac{{m}^{2}}{2+{m}^{2}})^{2}-\frac{{m}^{2}-16}{2+{m}^{2}}}$
=$\sqrt{\frac{(1+{m}^{2})(32+14{m}^{2})}{(2+{m}^{2})^{2}}}$,令t=2+m2(t≥2),
则|PQ|=$\sqrt{\frac{(t-1)(14t+4)}{{t}^{2}}}$=$\sqrt{-4(\frac{1}{t}+\frac{5}{4})^{2}+\frac{81}{4}}$,
当m=0即t=2时,取得最小值2$\sqrt{2}$,
即有2$\sqrt{2}$≤|PQ|<$\sqrt{14}$;
当直线l1:y=$\frac{1}{2}$时,代入椭圆方程,可得x=±$\frac{\sqrt{14}}{2}$,
即有|PQ|=$\sqrt{14}$.
综上可得,|PQ|的最大值为$\sqrt{14}$,此时直线方程为y=$\frac{1}{2}$.
点评 本题考查椭圆的方程的求法,注意运用椭圆的性质,考查点到直线的距离公式,以及联立直线方程和椭圆方程,运用韦达定理和弦长公式,化简整理的运算能力,属于中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 4S | B. | 4πS | C. | πS | D. | 2πS |
| A. | 0<a<1 | B. | 1<a<2 | C. | 1<a<$\frac{5}{2}$ | D. | 2<a<3 |
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
| A. | 9,7 | B. | 8,7 | C. | 9,8 | D. | 17,8 |
| A. | [0,2] | B. | [0,1] | C. | [0,$\frac{1}{2}$] | D. | [0,$\frac{1}{3}$] |