题目内容
2.已知函数f(x)=|lgx|,若$f(a)=f(b)=2f(\frac{a+b}{2})(0<a<b)$,则b所在区间为( )| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
分析 画出函数f(x)=|lgx|的图象,①设$\frac{a+b}{2}≥1$,由$f(a)=f(b)=2f(\frac{a+b}{2})(0<a<b)$,则-lga=lgb=2$lg\frac{a+b}{2}$,可得b=$(\frac{\frac{1}{b}+b}{2})^{2}$,化为:f(b)=b4-4b3+2b2+1=0,(b>1).利用导数研究其单调性即可得出;②设0<$\frac{a+b}{2}$<1,同理可得.
解答 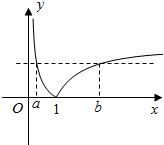 解:画出函数f(x)=|lgx|的图象,
解:画出函数f(x)=|lgx|的图象,
①设$\frac{a+b}{2}≥1$,∵$f(a)=f(b)=2f(\frac{a+b}{2})(0<a<b)$,
则-lga=lgb=2$lg\frac{a+b}{2}$,
ab=1,可得a=$\frac{1}{b}$,
则b=$(\frac{\frac{1}{b}+b}{2})^{2}$,
化为:f(b)=b4-4b3+2b2+1=0,(b>1).
f′(b)=4b(b2-3b+1)=4b$(b-\frac{3+\sqrt{5}}{2})$$(b-\frac{3-\sqrt{5}}{2})$,
可知:当b∈(1,$\frac{3+\sqrt{5}}{2}$)时,f′(b)<0,f(b)的单调递减;当b$>\frac{3+\sqrt{5}}{2}$时,f′(b)>0,f(b)的单调递增.
由f(1)=0,可知:$f(\frac{3+\sqrt{5}}{2})$<0,而f(3)=-8<0,f(4)=33>0,
∴此时存在唯一零点b∈(3,4).
②设0<$\frac{a+b}{2}$<1,∵$f(a)=f(b)=2f(\frac{a+b}{2})(0<a<b)$,
则-lga=lgb=-2$lg\frac{a+b}{2}$,
∴ab=1,$\frac{1}{b}$=$(\frac{a+b}{2})^{2}$,
化为:f(b)=b4+2b2-4b+1=0,(2>b>1).
f′(b)=2(2b3+b-2)>0,
可知:当b∈(1,2)时,函数f(b)的单调递增.
由f(1)=0,f(b)>0,此时函数f(b)不存在零点.
综上可得:b所在区间为(3,4).
故选:D.
点评 本题考查了利用导数研究函数的单调性极值与最值、函数的图象与性质,考查了推理能力与计算能力,属于难题.

| A. | $\frac{1}{7}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{3}$ |
| A. | 2 | B. | $\frac{2015}{2016}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{1}{2}$ |
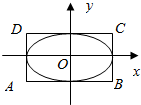 如图,椭圆 M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{1}{2}$,直线x=±a和y=±b所围成的矩形 A BCD的面积为$32\sqrt{3}$.
如图,椭圆 M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{1}{2}$,直线x=±a和y=±b所围成的矩形 A BCD的面积为$32\sqrt{3}$.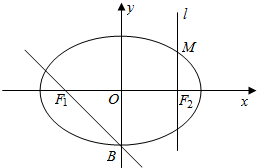 如图:在直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点分别为F1、F2.过右焦点F2与x轴垂直的直线l与椭圆C相交,其中一个交点为$M(\sqrt{2},1)$.
如图:在直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点分别为F1、F2.过右焦点F2与x轴垂直的直线l与椭圆C相交,其中一个交点为$M(\sqrt{2},1)$.