题目内容
9.已知F1,F2为椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1的左、右焦点,点E是椭圆C上的动点,$\overrightarrow{EF}$1•$\overrightarrow{EF}$2的最大值、最小值分别为( )| A. | 9,7 | B. | 8,7 | C. | 9,8 | D. | 17,8 |
分析 设出点E的坐标,进而可表示出$\overrightarrow{EF}$1,$\overrightarrow{EF}$2,运用向量的数量积的坐标表示和x的范围确定$\overrightarrow{EF}$1•$\overrightarrow{EF}$2的最值.
解答 解:由椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1可得a=3,b=2$\sqrt{2}$,c=$\sqrt{{a}^{2}-{b}^{2}}$=1,
知F1(-1,0),F2(1,0),
设E(x,y),即有$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1,即y2=8(1-$\frac{{x}^{2}}{9}$),
则 $\overrightarrow{EF}$1=(-1-x,-y),$\overrightarrow{EF}$2=(1-x,-y),
$\overrightarrow{EF}$1•$\overrightarrow{EF}$2=(-1-x)(1-x)+y2
=x2+y2-1=7+$\frac{{x}^{2}}{9}$,
∵x∈[-3,3],∴0≤x2≤9,
故$\overrightarrow{EF}$1•$\overrightarrow{EF}$2的最大值∈[7,8]
故最大值8,最小值7.
故选:B.
点评 本题主要考查了椭圆的应用.解答的关键是运用平面向量的数量积的坐标表示.考查运算能力,属于中档题.

练习册系列答案
相关题目
3.过点P(1,2)作圆(x+1)2+(y+1)2=1的两条切线,切点分别为A,B,则$\overrightarrow{PA}$•$\overrightarrow{PB}$=( )
| A. | $\frac{121}{12}$ | B. | $\frac{125}{12}$ | C. | $\frac{131}{13}$ | D. | $\frac{132}{13}$ |
14.设F1、F2分别是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左、右焦点,P为椭圆上任一点,点M的坐标为(6,4),则PM+PF1的最大值为15.
18.给定映射f:(x,y)→(2x+y,x-2y),在映射f下,(3,-1)的原像为( )
| A. | (-1,3) | B. | (5,5) | C. | (3,-1) | D. | (1,1) |
19.点P(1,2,3)到原点的距离是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | $\sqrt{14}$ | D. | 2 |
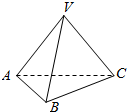 如图,三棱锥V-ABC的底面ABC为正三角形,侧面VAC与底面ABC垂直,且VA=VC,以平面VAC为正视图的投影面,其正视图的面积为$\frac{2}{3}$,则其侧视图的面积为$\frac{\sqrt{3}}{3}$.
如图,三棱锥V-ABC的底面ABC为正三角形,侧面VAC与底面ABC垂直,且VA=VC,以平面VAC为正视图的投影面,其正视图的面积为$\frac{2}{3}$,则其侧视图的面积为$\frac{\sqrt{3}}{3}$.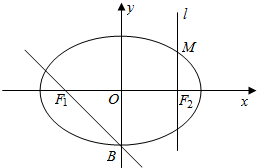 如图:在直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点分别为F1、F2.过右焦点F2与x轴垂直的直线l与椭圆C相交,其中一个交点为$M(\sqrt{2},1)$.
如图:在直角坐标系xoy中,设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点分别为F1、F2.过右焦点F2与x轴垂直的直线l与椭圆C相交,其中一个交点为$M(\sqrt{2},1)$.