题目内容
10.已知曲线C:y=x+$\frac{1}{x}$(1)求证:曲线C上的各点处的切线的斜率小于1;
(2)求曲线C上斜率为0的切线方程.
分析 (1)求导y′=1-$\frac{1}{{x}^{2}}$<1,从而可判断函数y=x+$\frac{1}{x}$图象上各点处切线的斜率都小于1.
(2)令y′=1-$\frac{1}{{x}^{2}}$=0得x=±1,从而由导数的几何意义求切线方程.
解答 解:(1)证明:∵y=x+$\frac{1}{x}$,
∴y′=1-$\frac{1}{{x}^{2}}$<1,
即对函数y=x+$\frac{1}{x}$定义域内的任一x,其导数值都小于1,
由导数的几何意义可知,
函数y=x+$\frac{1}{x}$图象上各点处切线的斜率都小于1.
(2)令y′=1-$\frac{1}{{x}^{2}}$=0,得x=±1,
当x=1时,y=1+1=2;
当x=-1时,y=-2,
∴曲线y=x+$\frac{1}{x}$的斜率为0的切线有两条,其切点分别为(1,2)与(-1,-2),
切线方程分别为y=2或y=-2.
点评 本题考查了导数的几何意义与导数的综合应用,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
5.设A={x|y=$\sqrt{2-x}$},B={x|x-a<0},若A∩B=A,则实数a的取值范围是( )
| A. | a>2 | B. | a≥2 | C. | a<2 | D. | a≤2 |
15.过点(0,8)作曲线f(x)=x3-6x2+9x的切线,则这样的切线条数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
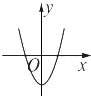 B、
B、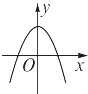 C、
C、 D、
D、