题目内容

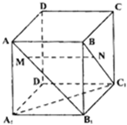
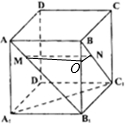
如图，正方体ABCD-A1B1C1D1棱长为1，点M∈AB1，N∈BC1，且AM=BN≠
2
，有以下四个结论：
①AA1⊥MN，②A1C1∥MN；③MN∥平面A1B1C1D1；④MN与A1C1是异面直线．其中正确结论的序号是______（注：把你认为正确命题的序号都填上）
过M作MO∥AB，交BB1于O，连接ON，
∵AM=BN
∴
AM
MB1
=
BO
OB1
=
BN
NC1
，∴ON∥B1C1，
∴BB1⊥OM，BB1⊥ON，OM∩ON=O，
∴BB1⊥平面OMN，MN?平面OMN，
∴BB1⊥MN，AA1∥BB1，∴AA1⊥MN，∴①正确；
当M、N分别是AB1，BC1的中点时，取A1B1，B1C1的中点E，F，连接ME、NF，
∵ME∥AA1，NF∥AA1，且ME=NF=
1
2
AA1，
∴四边形MNEF为平行四边形，∴MN∥EF，
又EF∥A1C1，∴MN∥A1C1，
当M不是AB1的中点时，MN与A1C1异面，∴②④错误；
OM∥平面A1B1C1D1；ON∥平面A1B1C1D1，
∴平面A1B1C1D1∥平面OMN，MN?平面OMN，
∴MN∥平面A1B1C1D1；∴③正确．
故答案是①③．
练习册系列答案
相关题目
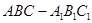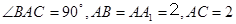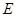如图,直三棱柱中, ,为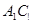中点，求直线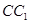与平面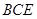所成角的大小.（结果用反三角函数值表示）
如图所示，ABCD-A1B1C1D1是长方体，O是B1D1的中点，直线A1C交平面AB1D于点M，则下列结论正确的是（　　）
A．A，M，O三点共线B．A，M，OA1不共面
C．A，M，C，O不共面D．B，B1，O，M共面
在直三棱柱ABC-A1B1C1中，BC1⊥A1C．有下列条件：
①AB=AC=BC；②AB⊥AC；③AB=AC．其中能成为BC1⊥AB1的充要条件的是（填上该条件的序号）______．
设P表示一个点，a，b表示两条直线，α，β表示两个平面，给出下列四个命题，其中正确的命题是（　　）
①P∈a，P∈α⇒a?α
②a∩b=P，b?β⇒a?β
③a∥b，a?α，P∈b，P∈α⇒b?α
④α∩β=b，P∈α，P∈β⇒P∈b．
A．①②B．②③C．①④D．③④
平行于同一个平面的两条直线，它们的空间位置关系为（　　）
A．平行B．相交
C．异面D．以上三种均有可能
已知两个不同的平面α，β和两条不重合的直线m，n，则下列命题正确的是（　　）
A．若m∥α，n∥β，α∥β，则m∥nB．若m∥α，α∩β=n，则m∥n
C．若m∥n，m?α，n?β，则α∥βD．若m?α，n?α，m∥n，则m∥α
已知a、β是不重合的平面，a、b、c是不重合的直线，给出下列命题：
①
a⊥α
a?β
②
a⊥b
c⊥b
⇒a∥c③
a∥α
b⊥a
⇒b⊥α
其中正确命题的个数是（　　）
A．3B．2C．1D．0
在正方形SG1G2G3中，E、F分别是G1G2及G2G3的中点，D是EF的中点，现在沿SE、SF及EF把这个正方形折成一个四面体，使G1、G2、G3三点重合，重合后的点记为G，那么，在四面体S-EFG中必有（　　）
A．SG⊥△EFG所在平面B．SD⊥△EFG所在平面
C．GF⊥△SEF所在平面D．GD⊥△SEF所在平面

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网