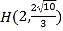题目内容
【题目】在平面直角坐标系
中，已知曲线
（
为参数），以坐标原点
为极点，
轴的非负半轴为极轴建立极坐标系，直线
的极坐标方程为：
.
（1）求直线和曲线
的直角坐标方程；
（2）
，直线和曲线交于
、
两点，求
的值.
【答案】（1）
，
；（2）
.
【解析】
（1）在曲线
的参数方程中消去参数
，可得出曲线的直角坐标方程，将直线
的极坐标方程变形为
，代入公式
可将直线的极坐标方程化为直角坐标方程；
（2）写出直线的参数方程，设
、
对应的参数分别为
、
，将直线的参数方程与曲线的普通方程联立，列出韦达定理，进而可求得
的值.
（1）由
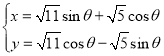得
，
所以，曲线的直角坐标方程为
.
直线的极坐标方程可变形为，
所以直线的直角坐标方程为
；
（2）直线的参数坐标方程为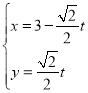
（
为参数）.
设、对应的参数分别为、，
将直线的参数方程代入，得
，
，
.
.
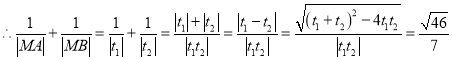千里马走向假期期末仿真试卷寒假系列答案
【题目】有甲、乙两个班级进行数学考试，按照大于或等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的2×2列联表．已知从全部210人中随机抽取1人为优秀的概率为
.
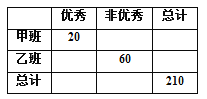
(1)请完成上面的2×2列联表，并判断若按99%的可靠性要求，能否认为“成绩与班级有关”；
(2)从全部210人中有放回地抽取3次，每次抽取1人，记被抽取的3人中的优秀人数为ξ，若每次抽取的结果是相互独立的，求ξ的分布列及数学期望E(ξ)．
P(K2≥k0) | 0.05 | 0.01 |
k0 | 3.841 | 6.635 |
附：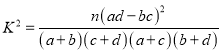 
【题目】某市垃圾处理厂的垃圾年处理量（单位：千万吨）与资金投入量x（单位：千万元）有如下统计数据：
2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
资金投入量x（千万元） | 1.5 | 1.4 | 1.9 | 1.6 | 2.1 |
垃圾处理量y（千万吨） | 7.4 | 7.0 | 9.2 | 7.9 | 10.0 |
（1）若从统计的5年中任取2年，求这2年的垃圾处理量至少有一年不低于8.0（千万吨）的概率；
（2）由表中数据求得线性回归方程为
，该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨，现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元，请你预测2017年能否完成垃圾处理任务，若不能，缺口约为多少千万吨？
