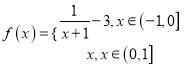题目内容
【题目】有甲、乙两个班级进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表.已知从全部210人中随机抽取1人为优秀的概率为![]() .
.
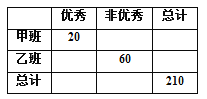
(1)请完成上面的2×2列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
(2)从全部210人中有放回地抽取3次,每次抽取1人,记被抽取的3人中的优秀人数为ξ,若每次抽取的结果是相互独立的,求ξ的分布列及数学期望E(ξ).
P(K2≥k0) | 0.05 | 0.01 |
k0 | 3.841 | 6.635 |
附: 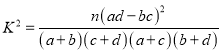
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)优秀人数为![]() ,进而求得其它数据,从而求得
,进而求得其它数据,从而求得![]() ,故可以判定有关;(2)易得
,故可以判定有关;(2)易得![]() ,计算得分布列及方差.试题解析:
,计算得分布列及方差.试题解析:
(1)
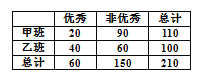
k≈12.2,所以按照99%的可靠性要求,能够判断成绩与班级有关.
(2)ξ~B![]() ,且P(ξ=k)=C
,且P(ξ=k)=C![]() k·
k·![]() 3-k(k=0,1,2,3),ξ的分布列为
3-k(k=0,1,2,3),ξ的分布列为
![]()
E(ξ)=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目