题目内容
三棱柱 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 内的射影为
内的射影为 的中心
的中心 ,则
,则 与底面
与底面 所成角的正弦值等于( )
所成角的正弦值等于( )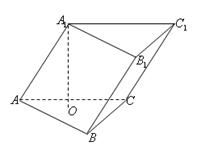
A. | B. |
C. | D. |
A
解析试题分析:先求出点A1到底面的距离A1D的长度,即知点B1到底面的距离B1E的长度,再求出AE的长度,在直角三角形AEB1中求AB1与底面ABC所成角的正切,再由同角三角函数的关系求出其正弦。由题意不妨令棱长为2,如图,A1在底面ABC内的射影为△ABC的中心,故 ,则由勾股定理可知
,则由勾股定理可知 ,
, ,如图作A1S⊥AB于中点S,易得A1S=
,如图作A1S⊥AB于中点S,易得A1S=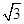 ,所以
,所以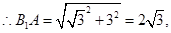 ,故所以AB1与底面ABC所成角的正弦值sin∠B1AE
,故所以AB1与底面ABC所成角的正弦值sin∠B1AE ,故选A.
,故选A.
考点:线面角的求解
点评:本题考查了几何体的结构特征及线面角的定义,还有点面距与线面距的转化,考查了转化思想和空间想象能力.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
若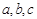 是空间三条不同的直线,
是空间三条不同的直线,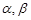 是空间两个不同的平面,则下列命题中,逆命题不正确的是( )
是空间两个不同的平面,则下列命题中,逆命题不正确的是( )
A.当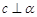 时,若 时,若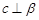 ,则 ,则 |
B.当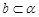 时,若 时,若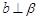 ,则 ,则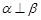 |
C.当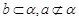 且 且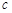 是 是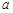 在 在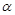 内的射影时,若 内的射影时,若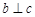 ,则 ,则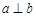 |
D.当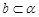 且 且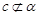 时,若 时,若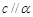 ,则 ,则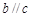 |
在空间,下列命题正确的是( )
| A.平行直线在同一平面内的射影平行或重合 | B.垂直于同一平面的两条直线平行 |
| C.垂直于同一平面的两个平面平行 | D.平行于同一直线的两个平面平行 |
设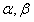 为两个平面,
为两个平面,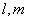 为两条直线,且
为两条直线,且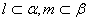 ,有如下两个命题:
,有如下两个命题:
①若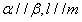 ;②若
;②若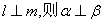 . 那么( )
. 那么( )
| A.①是真命题,②是假命题 | B.①是假命题,②是真命题 |
| C.①、②都是真命题 | D.①、②都是假命题 |
在正方体 中,直线
中,直线 与平面
与平面 所成的角的大小为( )
所成的角的大小为( )
| A.900 | B.600 | C.450 | D.300 |
 是平面,
是平面,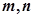 是直线,给出下列命题,其中正确的命题的个数是( )
是直线,给出下列命题,其中正确的命题的个数是( ) ,则
,则
 ,则
,则
 是异面直线,那么
是异面直线,那么 与
与 相交
相交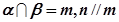 ,且
,且 ,则
,则 且
且 .
.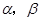 截球O的两个截面圆的半径分别为1和
截球O的两个截面圆的半径分别为1和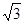 .若二面角
.若二面角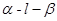 的平面角为150°,则球O的表面积为
的平面角为150°,则球O的表面积为
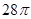
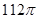
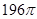
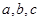 是三条不同的直线,
是三条不同的直线,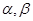 是两个不同的平面,在下列命题:
是两个不同的平面,在下列命题: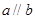 ,且
,且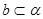 ,则
,则
 ,且
,且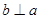 ,则
,则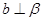
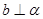 ,则
,则


