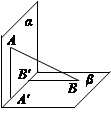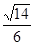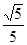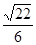题目内容
若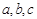 是空间三条不同的直线,
是空间三条不同的直线,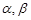 是空间两个不同的平面,则下列命题中,逆命题不正确的是( )
是空间两个不同的平面,则下列命题中,逆命题不正确的是( )
A.当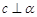 时,若 时,若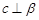 ,则 ,则 |
B.当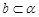 时,若 时,若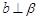 ,则 ,则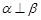 |
C.当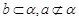 且 且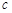 是 是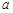 在 在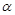 内的射影时,若 内的射影时,若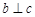 ,则 ,则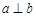 |
D.当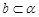 且 且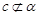 时,若 时,若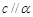 ,则 ,则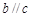 |
B
解析试题分析:A逆命题:当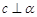 时,若
时,若 则
则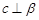 是真命题;B逆命题:当
是真命题;B逆命题:当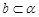 时,若
时,若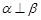 则
则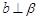 是假命题,只有当
是假命题,只有当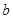 垂直于交线时命题才成立;C逆命题:当
垂直于交线时命题才成立;C逆命题:当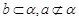 且
且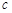 是
是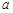 在
在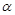 内的射影时,若
内的射影时,若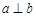 则
则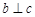 是真命题;D逆命题:当
是真命题;D逆命题:当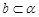 且
且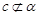 时若
时若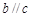 则
则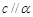 是真命题
是真命题
考点:空间线面平行垂直的判定和性质及四种命题
点评:逆命题是将原命题的条件和结论交换后构成的命题,空间线面的位置关系的判定属于基本知识点的考查,要求学生熟记掌握判定定理和性质定理

练习册系列答案
相关题目
下列命题中正确的个数是( )
①若直线a不在α内,则a∥α;
②若直线l上有无数个点不在平面α内,则l∥α;
③若直线l与平面α平行,则l与α内的任意一条直线都平行;
④若l与平面α平行,则l与α内任何一条直线都没有公共点;
⑤平行于同一平面的两直线可以相交.
| A.1 | B.2 | C.3 | D.4 |
已知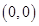 ,
,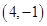 两点到直线
两点到直线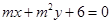 的距离相等,那么
的距离相等,那么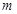 可取得不同实数值个数为( )
可取得不同实数值个数为( )
| A.1 | B.2 | C.3 | D.4 |
已知长方体ABCD—A1B1ClD1内接于球O,底面ABCD是边长为2的正方形,E为AA1的中点,OA⊥平面BDE,则球O的表面积为
A.8 | B.16 : : | C.14 | D.18 |
三条直线相交于一点,可能确定的平面有
A.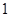 个 个 | B.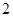 个 个 | C.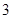 个 个 | D.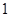 个或 个或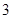 个 个 |
如图,四面体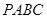 的六条边均相等,
的六条边均相等,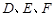 分别是
分别是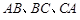 的中点,则下列四个结论中不成立的是 ( )
的中点,则下列四个结论中不成立的是 ( ) 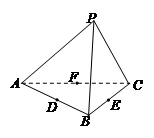
A.平面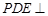 平面 平面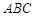 | B.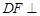 平面 平面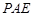 |
C. //平面 //平面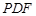 | D.平面 平面 平面 |
三棱柱 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 内的射影为
内的射影为 的中心
的中心 ,则
,则 与底面
与底面 所成角的正弦值等于( )
所成角的正弦值等于( )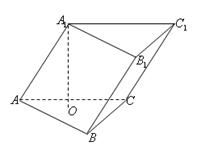
A. | B. |
C. | D. |
 的棱线长为1,面对角线
的棱线长为1,面对角线 上有两个动点E,F,且
上有两个动点E,F,且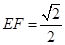 ,则下列四个结论中①
,则下列四个结论中①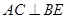 ②
②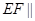 平面
平面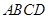 ③三棱锥
③三棱锥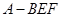 的体积为定值 ④异面直线
的体积为定值 ④异面直线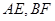 所成的角为定值,其中正确的个数是
所成的角为定值,其中正确的个数是 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,若
,过A、B分别作两平面交线的垂线,垂足为A′、B′,若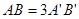 ,则AB与平面β所成的角的正弦值是( )
,则AB与平面β所成的角的正弦值是( )