题目内容
直线l与球O有且只有一个公共点P,从直线l出发的两个半平面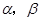 截球O的两个截面圆的半径分别为1和
截球O的两个截面圆的半径分别为1和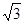 .若二面角
.若二面角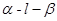 的平面角为150°,则球O的表面积为
的平面角为150°,则球O的表面积为
A. | B.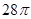 | C.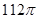 | D.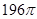 |
C
解析试题分析:欲求球O的表面积,只需求出球O的半径,根据题意OP长即球O的半径,再根据球心与截面圆圆心连线垂直截面圆,可考虑连接球心与两个截面圆圆心,利用得到的图形中的一些边角关系,求出R,再利用球的表面积公式即可求出球O的表面积.
解:设平面α,β截球O的两个截面圆的圆心分别为A,B,
连接PA,PB,与球交点为C,D根据题意在四边形OAPB中,∠APB=150°,∠OAP=∠OBP=90°
∴∠AOB=30°,PA=1,PB=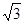 ,那么小圆的直径分别是2,和2
,那么小圆的直径分别是2,和2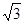 ,那么结合角∠APB=150°,运用余弦定理得到得到为CD=2
,那么结合角∠APB=150°,运用余弦定理得到得到为CD=2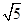 ,而球的半径就是三角形PAB的外接圆的半径,则利用正弦定理可知为球的半径为2
,而球的半径就是三角形PAB的外接圆的半径,则利用正弦定理可知为球的半径为2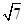 ,因此球的表面积为
,因此球的表面积为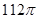 ,故选C.
,故选C.
考点:球的表面积
点评:本题考查了球的截面圆的性质,以及二面角的平面角的找法,综合性较强,做题时要认真分析,找到联系.

练习册系列答案
相关题目
三条直线相交于一点,可能确定的平面有
A.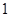 个 个 | B.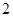 个 个 | C.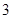 个 个 | D.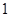 个或 个或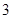 个 个 |
设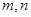 为两条不同的直线,
为两条不同的直线, 是两个不同的平面,下列命题正确的是
是两个不同的平面,下列命题正确的是
A.若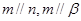 ,则 ,则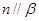 | B.若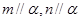 ,则 ,则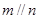 |
C.若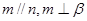 ,则 ,则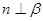 | D.若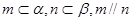 ,则 ,则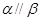 |
如图,在长方体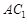 中,
中, ,
,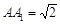 ,
,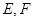 分别是面
分别是面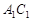 ,面
,面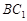 的中心,则
的中心,则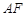 和
和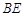 所成的角为( )
所成的角为( )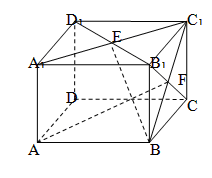
A.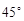 | B.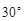 | C.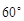 | D.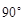 |
三棱柱 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 内的射影为
内的射影为 的中心
的中心 ,则
,则 与底面
与底面 所成角的正弦值等于( )
所成角的正弦值等于( )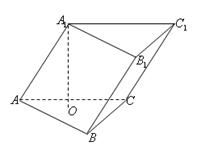
A. | B. |
C. | D. |
已知两个不同的平面α, 和两条不重合的直线m,n,则下列四种说法正确的为( )
和两条不重合的直线m,n,则下列四种说法正确的为( )
A.若m∥n,n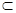 α,则m∥α α,则m∥α |
| B.若m⊥n,m⊥α,则n∥α |
C.若m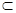 α,n α,n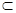  ,α∥ ,α∥ ,则m,n为异面直线 ,则m,n为异面直线 |
D.若α⊥ ,m⊥α,n⊥ ,m⊥α,n⊥ ,则m⊥n ,则m⊥n |
设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
A.若m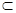 α,n α,n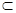 β,m∥n,则α∥β β,m∥n,则α∥β |
| B.若n⊥α,n⊥β,m⊥β,则m⊥α |
| C.若m∥α,n∥β,m⊥n,则α⊥β |
| D.若α⊥β,n⊥β,m⊥n,则m⊥α |
已知两条不同的直线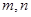 ,两个不同的平面
,两个不同的平面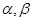 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.若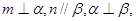 则 则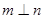 |
B.若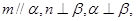 则 则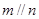 |
C.若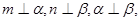 则 则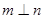 |
D.若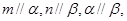 则 则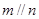 |
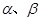 表示两个互相垂直的平面,
表示两个互相垂直的平面,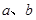 表示一对异面直线,则
表示一对异面直线,则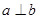 的一个充分条件是( )
的一个充分条件是( )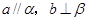 B.
B.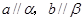
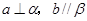 D.
D.