题目内容
18.在区间[-3,3]上随机取一个数x,使得$\frac{3-x}{x+1}$≥0成立的概率为$\frac{2}{3}$.分析 由题意,本题符合几何概型,只要求出区间的长度以及使不等式成立的x的范围区间长度,利用几何概型公式可得.
解答 解:由题意,本题符合几何概型,区间[-3,3]长度为6,使得$\frac{3-x}{x+1}$≥0成立的x的范围为(-1,3],区间长度为4,
由几何概型公式可得使得$\frac{3-x}{x+1}$≥0成立的概率为:$\frac{4}{6}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查了几何概型公式的运用;关键是明确所求是区间长度的比.

练习册系列答案
相关题目
6.已知α,β 表示平面,m,n表示直线,给出下列四个命题:
①若α∥β,m?α,n?β,则m∥n; ②若α⊥β,m?α,n?β,则m⊥n;
③若m⊥α,n⊥β,m∥n,则α∥β; ④若m∥α,n∥β,m⊥n,则α⊥β.
其中错误的命题个数为( )
①若α∥β,m?α,n?β,则m∥n; ②若α⊥β,m?α,n?β,则m⊥n;
③若m⊥α,n⊥β,m∥n,则α∥β; ④若m∥α,n∥β,m⊥n,则α⊥β.
其中错误的命题个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.已知过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的中心的直线交双曲线于点A,B,在双曲线C上任取与点A,B不重合的点P,记直线PA,PB,AB的斜率分别为k1,k2,k,若k1k2>k恒成立,则离心率e的取值范围为( )
| A. | 1<e<$\sqrt{2}$ | B. | 1<e≤$\sqrt{2}$ | C. | e>$\sqrt{2}$ | D. | e≥$\sqrt{2}$ |
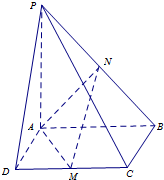 如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.
如图4,已知四棱锥P-ABCD,底面ABCD是正方形,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM,AN,MN.
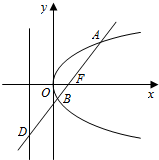 已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点.
已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点.